��Ŀ����
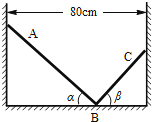
����Ŀ����ͼ��һ���뾶ΪR�İ����ε���̶��������ϣ����ˮƽ��O��Ϊ�����ģ�����ڱ��漰����ǹ⻬�ģ�һ������ϸ�߿�������ϣ��ߵ����˷ֱ�ϵ��С��A��B �� �����Ǵ���ƽ��״̬ʱ��С��A��O���������ˮƽ�ߵļн�Ϊ60�㣮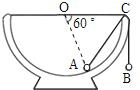
��1������A����B��������mA��mB
��2���ֽ�A��������Ϊ2m��B��������Ϊm �� �ҿ�ʼʱA��λ�����C�㣬�ɾ�ֹ�����»�����A�����ʱ���������ܵ��������ܸı�������B��δ������ڣ�
��3���ڣ�2�������£���A�����ʱ����B����ٶȴ�С��
���𰸡�
��1��
����������ΪT����A�����������������:
Nsin60��+Tsin60��=mAg
Ncos60��=Tcos60��
��B����������������� T=mBg
�ɽ�ã� ![]()
��2��
A����������ܸı���Ϊ��EpA=��mAgR=��2mgR��
B������������ܸı���Ϊ ![]()
����A��B�����ܵ��������ܸı���Ϊ ![]()
��3��
��A�����ʱ����A��B������ٶȷֱ�ΪvA��vB����vAcos45��=vB ��1��
����A��B�����ܻ�е���غ㣬����EK+��Ep=0 ��2��
�� ![]() ��3��
��3��
����������ʽ����ã� ![]() ����
���� ![]() ��
�� ![]() ��
��
����������1������������ΪT �� ��A�����������������:
Nsin60��+Tsin60��=mAg
Ncos60��=Tcos60��
��B����������������� T=mBg
�ɽ�ã� ![]() ��2��A����������ܸı���Ϊ��EpA=��mAgR=��2mgR
��2��A����������ܸı���Ϊ��EpA=��mAgR=��2mgR
B������������ܸı���Ϊ ![]()
����A��B�����ܵ��������ܸı���Ϊ ![]() ��3����A�����ʱ����A��B������ٶȷֱ�ΪvA��vB �� ��vAcos45��=vB��1��
��3����A�����ʱ����A��B������ٶȷֱ�ΪvA��vB �� ��vAcos45��=vB��1��
����A��B�����ܻ�е���غ㣬����EK+��Ep=0 ��2��
�� ![]() ��3��
��3��
����������ʽ����ã� ![]() ����
���� ![]() ��
�� ![]() ��
��

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�