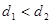题目内容
 质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.左侧射手首先开枪,子弹相对木块静止时水平射入木块的最大深度为d1,然后右侧射手开枪,子弹相对木块静止时水平射入木块的最大深度为d2,如图所示.设子弹均未射穿木块,且两颗子弹与木块之间的作用力大小均相等.当两颗子弹均相对于木块静止时,下列判断正确的是( )
质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.左侧射手首先开枪,子弹相对木块静止时水平射入木块的最大深度为d1,然后右侧射手开枪,子弹相对木块静止时水平射入木块的最大深度为d2,如图所示.设子弹均未射穿木块,且两颗子弹与木块之间的作用力大小均相等.当两颗子弹均相对于木块静止时,下列判断正确的是( )分析:对两颗子弹和木块组成的系统而言,合外力为零,总动量守恒,可求出当两颗子弹均相对于木块静止时木块的速度.先以左侧的子弹和木块组成的系统研究,由动量守恒和能量守恒得到d1与子弹速度、质量和木块的关系,再对两颗子弹和木块系统为研究,用同样的方法研究d2,再比较它们的大小.
解答:解:设子弹射入木块前的速度大小为v,子弹的质量为M,子弹受到的阻力大小为f.当两颗子弹均相对于木块静止时,由动量守恒得
mv-mv=(2m+M)v′,得v′=0,即当两颗子弹均相对于木块静止时,木块的速度为零,即静止.
先对左侧射入木块的子弹和木块组成的系统研究,则有
mv=(M+m)v1,
由能量守恒得:fd1=
mv2-
(M+m)
①
再对两颗子弹和木块系统为研究,得
fd2=
(M+m)
+
mv2②
由①②对比得,d1<d2.
故C正确.
mv-mv=(2m+M)v′,得v′=0,即当两颗子弹均相对于木块静止时,木块的速度为零,即静止.
先对左侧射入木块的子弹和木块组成的系统研究,则有
mv=(M+m)v1,
由能量守恒得:fd1=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
再对两颗子弹和木块系统为研究,得
fd2=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
由①②对比得,d1<d2.
故C正确.
点评:本题运用动量守恒和能量守恒相结合分析子弹与木块相对位移大小的关系,是常用的基本思路.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013?邵阳模拟)(供选学3-5模块的考生做)x质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用力大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )
(2013?邵阳模拟)(供选学3-5模块的考生做)x质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用力大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( ) 质量为M的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同的滑块的同学.首先左侧同学以大小为V的速度先水平向右扔出滑块,滑块在木板上滑行的最大距离为d1;然后右侧同学也以大小为v的速度水平向左扔出滑块,滑块在木板上滑行的最大距离为d2,如图所示.设两滑块在木板上没有相碰.当两滑块均相对木块静止时,下列说法正确的是( )
质量为M的均匀木块静止在光滑水平面上,木块左右两侧各有一位拿着完全相同的滑块的同学.首先左侧同学以大小为V的速度先水平向右扔出滑块,滑块在木板上滑行的最大距离为d1;然后右侧同学也以大小为v的速度水平向左扔出滑块,滑块在木板上滑行的最大距离为d2,如图所示.设两滑块在木板上没有相碰.当两滑块均相对木块静止时,下列说法正确的是( )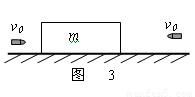
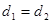 B.木块向右运动,
B.木块向右运动,