题目内容
如图所示，木块质量m＝0.78kg，在与水平方向成37°角、斜向右上方的恒定拉力F作用下，以a＝2.0m/s2的加速度从静止开始做匀加速直线运动，在3s末时撤去拉力F。已知木块与地面间的动摩擦因数m＝0.4，（sin37°＝0.60，cos37°＝0.80。）求：拉力F的大小以及物体在5s内滑行的总位移。
某同学是这样分析的：由牛顿第二定律可得Fcosq－mmg＝ma，可求出拉力F的大小。物体加速阶段滑行的时间t1＝3s，位移s1＝
at12，末速度v1＝at1，减速阶段滑行的时间t2＝2s，加速度a'＝mg，可求出位移s2，则滑行的总位移s＝s1＋s2。你认为这位同学的分析是否正确，若正确，请列式并完成计算；若不正确，请说明理由，并用你自己的方法算出正确的结果。
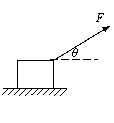
解：不正确。在外力F斜向上时摩擦力大小不等于μmg，而且物体在拉力撤去后继续滑行的时间不是2s。 （1分）
（1）N+Fsinθ = mg （1分）
Fcosθ-μN = ma （1分）
联立方程组，解得拉力
N （1分）
（2）匀加速阶段：
m （1分）
v1=at1=2×3=6m/s （1分）
匀减速阶段：a'= μg =0.4×10 = 4m/s2 （1分）
t2= v/a' = 6/4 =1.5s s2 = v1t2/2 = 6×1.5/2 = 4.5m （1分）
物体在5s内滑行的总位移s = s1+s2 = 9+4.5 = 13.5m （1分）
练习册系列答案
浙江名校名师金卷系列答案
相关题目
（2010?岳阳模拟）辨析题：如图所示，木块质量m=0.78kg，在与水平方向成37°角、斜向右上方的恒定拉力F作用下，以a=2.0m/s2的加速度从静止开始做匀加速直线运动，在3s末时撤去拉力F．已知木块与地面间的动摩擦因数μ=0.4，取重力加速度g=10m/s2，sin37°=0.60，cos37°=0.80．求：拉力F的大小以及物体在5s内滑行的总位移．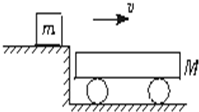
（2009?滨州模拟）如图所示，木块质量m=0.4kg，它以速度v=20m/s水平地滑上一辆静止的平板小车，已知小车质量M=1.6kg，木块与小车间的动摩擦因数为μ=0.2，木块没有滑离小车，地面光滑，g取10m/s2．
（2013?静安区一模）如图所示，木块质量m=1.04kg，在与水平方向成θ=37°角、斜向右上方的恒定拉力F作用下，以a=2.0m/s2的加速度从静止开始做匀加速直线运动，在3s末时撤去拉力F．已知木块与地面间的动摩擦因数μ=0.4，取重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．求：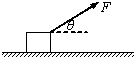
如图所示，木块质量m=0.78kg，在与水平方向成θ=37°角、斜向右上方的恒定拉力F作用下，以a=2.0m/s2的加速度从静止开始做匀加速直线运动，在3s末时撤去拉力F．已知木块与地面间的动摩擦因数μ=0.4，取重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．求：