题目内容
冰球运动员甲的质量为80.0kg。当他以5.0m/s的速度向前运动时,与另一质量为100kg、速度为3.0m/s的迎面而来的运动员乙相撞。碰后甲恰好静止。假设碰撞时间极短,求:
(1)碰后乙的速度的大小;
(2)碰撞中总机械能的损失。
(1)1.0m/s;(2)1400J
解析试题分析:(1)设运动员甲、乙的质量分别为m、M,碰前速度大小分别为v1、v2,碰后乙的速度大小为v′2,由动量守恒定律有:mv1-Mv2=Mv′2
解得:v′2= -v2=1.0m/s
-v2=1.0m/s
(2)根据能量守恒定律可知,碰撞中总机械能的损失为:ΔE=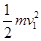 +
+ -
-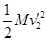
代入数据解得:ΔE=1400J
考点:本题主要考查了动量守恒定律和能量守恒定律的应用问题,属于中档题。

练习册系列答案
相关题目
如图所示,小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法中正确的是( )
| A.男孩和木箱组成的系统动量守恒 |
| B.男孩、小车与木箱三者组成的系统动量守恒 |
| C.小车与木箱组成的系统动量守恒 |
| D.木箱的动量增量与男孩、小车的总动量增量相同 |
质量为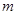 的物块甲以
的物块甲以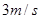 的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为
的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为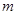 的物体乙以
的物体乙以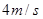 的速度与甲相向运动,如图所示。则
的速度与甲相向运动,如图所示。则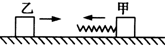
| A.甲、乙两物块在弹簧压缩过程中,由于弹力作用,动量不守恒 |
| B.当两物块相距最近时,物块甲的速率为零 |
| C.当物块甲的速率为1m/s时,物块乙的速率可能为2m/s,也可能为零 |
| D.物块甲的速率可能达到5m/s |

 ,碰撞前后打出的纸带如图(b)所示。
,碰撞前后打出的纸带如图(b)所示。
 最大为5℅,本实验是否在误差范围内验证了动量守恒定律?写出运算过程。
最大为5℅,本实验是否在误差范围内验证了动量守恒定律?写出运算过程。 初速度射入一个装有砂子的总质量为M的静止的砂车中并与车相对静止,砂车与水平地面间的摩擦可以忽略.求:
初速度射入一个装有砂子的总质量为M的静止的砂车中并与车相对静止,砂车与水平地面间的摩擦可以忽略.求: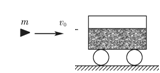
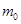 的砂子时砂车的速度
的砂子时砂车的速度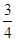 ,则抛出第四个沙包后,此车的运动情况如何?
,则抛出第四个沙包后,此车的运动情况如何?  的光滑水平圆形轨道,过圆心
的光滑水平圆形轨道,过圆心 相垂直的两虚线交圆弧于A、B、C、D四点,质量为
相垂直的两虚线交圆弧于A、B、C、D四点,质量为 的乙球静置于B处,质量为
的乙球静置于B处,质量为 的甲球从A处沿圆弧切线方向以速度
的甲球从A处沿圆弧切线方向以速度 开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求:
开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求: 
 ;
;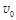 沿B、C的连线方向向B运动,求B球的质量M为何值时,才能使C球碰撞后的速度最大?(已知A、B、C之间的碰撞均为弹性碰撞)
沿B、C的连线方向向B运动,求B球的质量M为何值时,才能使C球碰撞后的速度最大?(已知A、B、C之间的碰撞均为弹性碰撞)