��Ŀ����
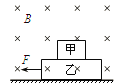
����Ŀ����ͼ��ʾ����ˮƽ�����Ϲ̶�һ�⻬�������죬��������ΪL��������費�ƣ��Ҷ˽�����ֵΪR�ĵ��裬����Ϊm������r=![]() R�ĵ������̶�������������ڵ����ϣ�����װ�ô��ڴŸ�Ӧǿ�ȴ�СΪB��������ֱ���µ���ǿ�ų��У���ʼʱ�̣�����ǡ������Ȼ���ȣ����������һˮƽ���ҵij��ٶ�v0 �� ��֪���������һ�λص���ʼλ��ʱ���ٶȴ�С��Ϊ
R�ĵ������̶�������������ڵ����ϣ�����װ�ô��ڴŸ�Ӧǿ�ȴ�СΪB��������ֱ���µ���ǿ�ų��У���ʼʱ�̣�����ǡ������Ȼ���ȣ����������һˮƽ���ҵij��ٶ�v0 �� ��֪���������һ�λص���ʼλ��ʱ���ٶȴ�С��Ϊ![]() v0�� �����˶������е����ʼ���뵼�崹ֱ���������ýӴ������ɵ����������뵼��ƽ�У��ҵ���ʼ�մ��ڵ����ȷ�Χ�ڣ���
v0�� �����˶������е����ʼ���뵼�崹ֱ���������ýӴ������ɵ����������뵼��ƽ�У��ҵ���ʼ�մ��ڵ����ȷ�Χ�ڣ���

��1����ʼʱ��ͨ������R�ĵ���I�Ĵ�С��
��2���������һ�λص���ʼλ��ʱ��������ļ��ٶȴ�СΪa��
��3��������ӿ�ʼ�˶�ֱ��ֹͣ�Ĺ����У�����R�ϲ����Ľ���Q��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
���⣨1����ʼʱ�̵�������ٶ�Ϊ![]() �����и�Ÿ����˶��������ĵ綯��Ϊ
�����и�Ÿ����˶��������ĵ綯��Ϊ![]() ��
��
��·�е��ܵ���Ϊ![]() ������ŷķ���ɿɵ�
������ŷķ���ɿɵ�![]()
��2���������һ�λص���ʼλ��ʱ���ٶ�Ϊ![]() �������ĵ���Ϊ
�������ĵ���Ϊ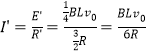
��ʱ���ɴ���ԭ��״̬������ֻ�ܰ��������ã�������Ϊ![]() ��
��
���� ţ�ٵڶ����ɿɵ�![]() ���������
���������![]()
��3������û��Ħ������������ӿ�ʼ�˶�ֱ��ֹͣ�Ĺ����У�������Ķ�����ȫת��Ϊ��·�Ľ����ȣ���![]() �����ݵ�·���ɿɵõ���R�ϲ����Ľ���
�����ݵ�·���ɿɵõ���R�ϲ����Ľ���![]() ��
��

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�