题目内容
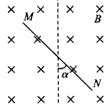
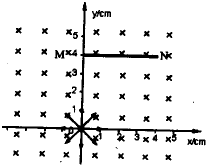 如图所示,空间存在垂直XOY平面向里的匀强磁场,MN为一荧光屏,上下两面均可发光,当带电粒子打到屏上某点时,即可使该点发光,荧光屏位置如图,坐标为M(0,4.0),N(4.0,4.0)单位为cm.坐标原点O有一粒子源,可以发射沿XOY平面各个方向的电子(不计电子的重力),已知电子质量m=9.0×10-31kg,电量为e=1.6×10-19C,磁感应强度B=9.0×10-3T,求:
如图所示,空间存在垂直XOY平面向里的匀强磁场,MN为一荧光屏,上下两面均可发光,当带电粒子打到屏上某点时,即可使该点发光,荧光屏位置如图,坐标为M(0,4.0),N(4.0,4.0)单位为cm.坐标原点O有一粒子源,可以发射沿XOY平面各个方向的电子(不计电子的重力),已知电子质量m=9.0×10-31kg,电量为e=1.6×10-19C,磁感应强度B=9.0×10-3T,求:(1)若一电子以v0=8.0×107m/s沿y轴正方向射入,求荧光屏上亮点坐标.
(2)若所有电子以v0=4.0×107m/s射入,求能打到M点的电子的速度入射方向.(用与X轴正方向的夹角或夹角的三角函数值表示)
(3)若所有电子以v0=4.0×107m/s射入,求荧光屏发光区域的坐标(坐标的单位为 cm).
分析:带电粒子以一定的速度进入匀强磁场,在洛伦兹力的作用下做匀速圆周运动.粒子在磁场中运动的周期仅与粒子的比荷有关,而运动的时间与偏转角有关.当入射速度越大时,运动轨道的半径越大.
解答:解:(1)qvB=
r=5×10-2m=5cm
由几何关系可知:r2=
+(r-x0)2
解得:x0=2cm坐标为(2,4)cm
(2)v0=4×107m/s r0=2.5cm,
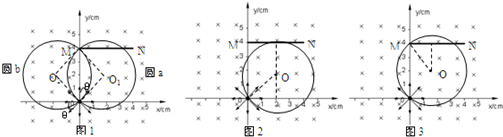
能打到M点的粒子轨迹如图1圆a和圆b所示
由几何关系:cosθ=
=0.8,
解得θ=37°
所以α1=180°-θ=143°,
α2=180°+θ=217°
(3)v0=4×107m/s r0=2.5cm,若打在下方最远点,如图2
所示为相切,由几何关系可知:
+(y0-r0)2
所以x0=2cm,坐标为(0,4)到(2,4)cm
若打在上方最远点,如图则轨迹圆左端刚好打在M点则:
+
=
所以x0=1.5cm 坐标为(0,4)到(3,4)cm
| mv2 |
| r |
r=5×10-2m=5cm
由几何关系可知:r2=
| y | 2 0 |
解得:x0=2cm坐标为(2,4)cm
(2)v0=4×107m/s r0=2.5cm,
能打到M点的粒子轨迹如图1圆a和圆b所示
由几何关系:cosθ=
| ||
| r0 |
解得θ=37°
所以α1=180°-θ=143°,
α2=180°+θ=217°
(3)v0=4×107m/s r0=2.5cm,若打在下方最远点,如图2
所示为相切,由几何关系可知:
| x | 2 0 |
| =r | 2 0 |
所以x0=2cm,坐标为(0,4)到(2,4)cm
若打在上方最远点,如图则轨迹圆左端刚好打在M点则:
| x | 2 0 |
| ||
| 2 |
| r | 2 0 |
所以x0=1.5cm 坐标为(0,4)到(3,4)cm

点评:带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径.

练习册系列答案
相关题目