题目内容
甲乙两位同学利用穿过打点计时器的纸带来记录小车的运动,打点计时器所用电源的频率为50Hz.
(1)实验后,甲同学选择了一条较为理想的纸带,测量数据后,通过计算得到了小车运动过程中各计时时刻的速度如表格所示.
分析表中数据,在误差允许的范围内,小车做______运动;由于此次实验的原始纸带没有保存,该同学想估算小车从位置0到位置5的位移,其估计算方法如下:x=(0.42×0.1+0.67×0.1+0.92×0.1+1.16×0.1+1.42×0.1)m,那么,该同学得到的位移______(选填“大于”、“等于”或“小于”)实际位移.
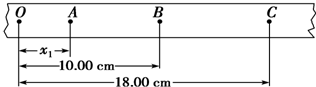
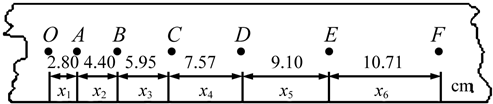
(2)乙同学的纸带如图1,按时间顺序取0、1、2、3、4、5、6七个计数点,每相邻的两计数点间都有四个点未画出.用刻度尺量出1、2、3、4、5、6点到0点的距离如图2所示(单位:cm).由纸带数据计算可得计数点3所代表时刻的瞬时速度大小v3=______m/s,小车的加速度大小a=______m/s2.

(1)实验后,甲同学选择了一条较为理想的纸带,测量数据后,通过计算得到了小车运动过程中各计时时刻的速度如表格所示.
| 位置编号 | 0 | 1 | 2 | 3 | 4 | 5 |
| 时间:t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 速度:v/m?s-1 | 0.42 | 0.67 | 0.92 | 1.16 | 1.42 | 1.76 |
(2)乙同学的纸带如图1,按时间顺序取0、1、2、3、4、5、6七个计数点,每相邻的两计数点间都有四个点未画出.用刻度尺量出1、2、3、4、5、6点到0点的距离如图2所示(单位:cm).由纸带数据计算可得计数点3所代表时刻的瞬时速度大小v3=______m/s,小车的加速度大小a=______m/s2.

(1)根据表中数据可知,小车的速度均匀增加,因此小车做匀加速直线运动;
小车做匀加速直线运动,0-0.1s实际位移应该大于0.42×0.1,依此类推0-0.4s实际位移应该大于0.42×0.1+0.67×0.1+0.92×0.1+1.16×0.1+1.42×0.1m,所以该同学得到的位移小于实际位移.
故答案为:匀加速直线,小于.
(2)由题意可知,相邻计数点间的时间间隔:t=0.02s×5=0.1s;
根据匀变速直线运动中时间中点的速度等于该过程中的点的瞬时速度,因此有:
v3=
=0.33m/s;
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值:
a=
=
代入数据解得:a=m/s2;
故答案为:0.33;0.76.
小车做匀加速直线运动,0-0.1s实际位移应该大于0.42×0.1,依此类推0-0.4s实际位移应该大于0.42×0.1+0.67×0.1+0.92×0.1+1.16×0.1+1.42×0.1m,所以该同学得到的位移小于实际位移.
故答案为:匀加速直线,小于.
(2)由题意可知,相邻计数点间的时间间隔:t=0.02s×5=0.1s;
根据匀变速直线运动中时间中点的速度等于该过程中的点的瞬时速度,因此有:
v3=
| x24 |
| 2T |
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值:
a=
| a1+a2+a3 |
| 3 |
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
代入数据解得:a=m/s2;
故答案为:0.33;0.76.

练习册系列答案
相关题目
 “中相应的数据填上.
“中相应的数据填上.