题目内容
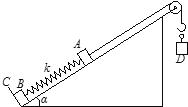
【题目】如图，光滑固定斜面倾角为α，斜面底端固定有垂直斜面的挡板C，斜面顶端固定有光滑定滑轮．质量为m的物体A经一轻质弹簧与下方挡板上的质量也为m的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态．一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩．开始时各段绳都处于伸直状态，A上方的一段绳平行于斜面．现在挂钩上挂一质量M的物体D并从静止状态释放，已知它恰好能使B离开挡板但不继续上升．若让D带上正电荷q，同时在D运动的空间中加上方向竖直向下的匀强电场，电场强度的大小为E，仍从上述初始位置由静止状态释放D，则这次B刚离开挡板时D的速度大小是多少？已知重力加速度为g.
【答案】
【解析】试题分析：挂钩没有挂D时，A压缩弹簧，弹簧的压缩量为
，对A有：
则：
（2分）
挂钩挂上D后，B刚好离开挡板时弹簧的伸长量为
，对B有：
则：
（2分）
该过程A沿斜面上升的距离和D下降的高度都是
，且A、D的初速度、末速度都为零。
设该过程弹性势能的增量为ΔE，由系统机械能守恒有
；（3分）
将D带电后，D在电场中运动，电场力对D作正功，设B刚离开挡板时D的速度为υ，D下降x1＋x2过程系统能量守恒，
有：
（3分）
由以上四个方程消去
，得：
（2分）
练习册系列答案
阅读快车系列答案
相关题目
