题目内容
13. 如图,位于一条直线上的三个点电荷A,B,C,其间隔为$\overline{AB}$=$\overline{BC}$=r,A和C都带正电荷,电荷量为q,在AC的垂直平分线上距B亦为r的P点,其场强恰为零,试确定点电荷B的电性和所带电荷量.
如图,位于一条直线上的三个点电荷A,B,C,其间隔为$\overline{AB}$=$\overline{BC}$=r,A和C都带正电荷,电荷量为q,在AC的垂直平分线上距B亦为r的P点,其场强恰为零,试确定点电荷B的电性和所带电荷量.
分析 根据库仑定律求出A与C在P点产生的场强,然后结合矢量的合成的方法求出AC在P点的合场强,则B在P点的场强与之大小相等,方向相反,由此即可判断出B点的点电荷的电性,最后有库仑定律即可求出电荷量.
解答 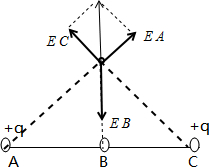 解:由几何关系可知,A和C到P的距离:$l=\sqrt{{\overline{AB}}^{2}+{\overline{BP}}^{2}}=\sqrt{{r}^{2}+{r}^{2}}=\sqrt{2}r$
解:由几何关系可知,A和C到P的距离:$l=\sqrt{{\overline{AB}}^{2}+{\overline{BP}}^{2}}=\sqrt{{r}^{2}+{r}^{2}}=\sqrt{2}r$
A与C在P点产生的场强的大小:${E}_{A}={E}_{C}=\frac{kq}{{l}^{2}}=\frac{kq}{2{r}^{2}}$
由图可知,A与C点的点电荷在P点产生的场强的方向相互垂直,合场强:E=$\sqrt{2}{E}_{A}=\frac{\sqrt{2}kq}{2{r}^{2}}$
由矢量的合成可知,B点的场强大小也是$\frac{\sqrt{2}kq}{2{r}^{2}}$,方向向下,所以B带负电.
由库仑定律:${E}_{B}=\frac{k{q}_{B}}{{r}^{2}}$
联立得:${q}_{B}=\frac{\sqrt{2}}{2}q$
答:B带负电,带电量大小是$\frac{\sqrt{2}}{2}q$.
点评 本题关键是明确电场强度是矢量,会根据平行四边形定则求解合场强,基础问题.

练习册系列答案
相关题目
4. 如图所示P和Q为两平行金属板,板间电压恒为U,在P板附近有一电子由静止开始向Q板运动,则关于电子在两板间运动情况,下列说法正确的是( )
如图所示P和Q为两平行金属板,板间电压恒为U,在P板附近有一电子由静止开始向Q板运动,则关于电子在两板间运动情况,下列说法正确的是( )
 如图所示P和Q为两平行金属板,板间电压恒为U,在P板附近有一电子由静止开始向Q板运动,则关于电子在两板间运动情况,下列说法正确的是( )
如图所示P和Q为两平行金属板,板间电压恒为U,在P板附近有一电子由静止开始向Q板运动,则关于电子在两板间运动情况,下列说法正确的是( )| A. | 两板间距离越大,加速时间越长 | |
| B. | 两板间距离越小,加速度越大,则电子到达Q板时获得的速率就越大 | |
| C. | 电子到达Q板时获得的速率与两板间距离无关,仅与加速电压U有关 | |
| D. | 电子的加速度和末速度都与两板间距离无关 |
1.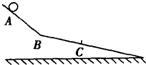 如图,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则球在AB、BC段的加速度大小之比及球由A运动到C过程中的平均速率分别为( )
如图,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则球在AB、BC段的加速度大小之比及球由A运动到C过程中的平均速率分别为( )
 如图,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则球在AB、BC段的加速度大小之比及球由A运动到C过程中的平均速率分别为( )
如图,两光滑斜面在B处连接,小球从A处由静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后速度大小不变,则球在AB、BC段的加速度大小之比及球由A运动到C过程中的平均速率分别为( )| A. | 3:4,2.1 m/s | B. | 9:16,2.5m/s | C. | 9:7,2.1m/s | D. | 9:7,2.5 m/s |
1.某人身高1.8m,欲买一镜子竖直挂在墙上能照见全身,镜子的最短长度和正确的悬挂方法是( )
| A. | 1.8m,镜子的顶边与头顶平齐 | |
| B. | 1.8m,镜子的顶边与双眼平齐 | |
| C. | 0.9m,镜子的顶边与双眼平齐 | |
| D. | 0.9m,镜子的顶边在头顶与双眼之间 |
19.质量为2kg的物体所受重力为(g=10m/s2)( )
| A. | 4N | B. | 40N | C. | 20N | D. | 30N |
 如图所示,用30cm的细线将质量为4×10-3kg的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为1×10-3N/C的匀强电场是,小球偏转37°后处于静止状态.(g=10N/kg)
如图所示,用30cm的细线将质量为4×10-3kg的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为1×10-3N/C的匀强电场是,小球偏转37°后处于静止状态.(g=10N/kg)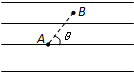 在如图所示的匀强电场中,有A、B两点,且A、B两点间的距离为x=0.20m,已知AB连线与电场线夹角为vD=$\sqrt{2}$v=60°,今把一电荷量q=-2×10-8C的检验电荷放入该匀强电场中,电场强度大小E=2×104V/m,方向水平向右.求:
在如图所示的匀强电场中,有A、B两点,且A、B两点间的距离为x=0.20m,已知AB连线与电场线夹角为vD=$\sqrt{2}$v=60°,今把一电荷量q=-2×10-8C的检验电荷放入该匀强电场中,电场强度大小E=2×104V/m,方向水平向右.求: