题目内容
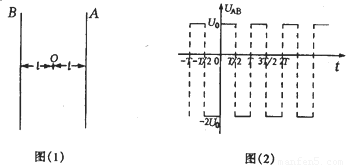
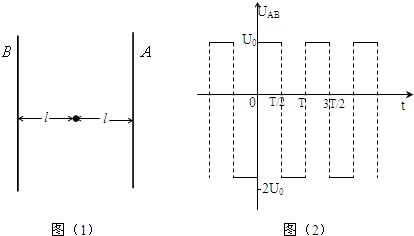
在图(1)中A和B是真空中的两块面积很大的平行金属板,A、B间的电压UAB随时间变化的规律如图(2)所示,在图(1)中O点到A和B的距离皆为l,在O处不断地产生电荷量为q、质量为m的带负电微粒,不计重力,不考虑微粒之间的相互作用,这种微粒产生后,从静止出发在电场力的作用下运动,设微粒一旦碰到金属板,就附在板上不再运动.且其电量同时消失,不影响A、B板间的电势.已知交变电压的周期T=6.0×10-3s.正电压为U0,负电压为-U0,且U0=6.0×102V,微粒电荷量q=2.0×10-7C,质量为m=1.0×10-9kg,l=0.3m.试求:
(1)在t=0时刻从静止出发的微粒,会在t1时刻到达极板,求t1的值?
(2)若在t=0到t=T/2这段时间内的某一时刻t2产生的微粒刚好不能到达A板,求t2的值?
(3)求t2时刻产生的微粒到达B板所需的时间?
(1)在t=0时刻从静止出发的微粒,会在t1时刻到达极板,求t1的值?
(2)若在t=0到t=T/2这段时间内的某一时刻t2产生的微粒刚好不能到达A板,求t2的值?
(3)求t2时刻产生的微粒到达B板所需的时间?

分析:(1)根据牛顿第二定律求出粒子的加速度,通过位移时间公式求出粒子到达极板的时间.
(2)在t=0到t=
这段时间内的t2时刻产生的微粒刚好不能到达A板,在此过程中,经历了匀加速直线运动和匀减速直线运动,抓住位移之和等于l,以及两段过程速度的关系,求出不能到达A板的时间.
(3)再经△t3=
-△t2时间微粒向左匀加速运动,其位移为s3=
a2△
,粒子再经△t4微粒减速运动S4碰到B板.s4=2l-S3.由运动学公式:s4=a2△t3?△t4-
a1
代入数据可解得△t4,则微粒运动到B板的总时间为t=△t1+△t2+△t3+△t4.
(2)在t=0到t=
| T |
| 2 |
(3)再经△t3=
| T |
| 2 |
| 1 |
| 2 |
| t | 2 3 |
| 1 |
| 2 |
| t | 2 4 |
代入数据可解得△t4,则微粒运动到B板的总时间为t=△t1+△t2+△t3+△t4.
解答: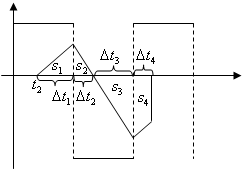 解:
解:
(1)当电压为U0时,微粒的加速度a1=
=1×105m/s2
微粒向A板做匀加速运动,位移l=
a1
解得t1=
×10-3s<
所以在t=0时刻从静止出发的微粒,会在
×10-3s时刻到达A极板.
(2)当电压为2U0时,微粒的加速度a2=
=2×105m/s2
微粒先经△t1时间加速,再经△t2时间恰好到达A板,速度减为零.位移分别为S1、S2
加速的位移s1=
a1△
减速的加速度为加速的加速度的2倍,所以减速的位移s2=
S1
加速的末速度等于减速的初速度,所以a2△t=a1△t1
又因为l=S1+S2
代入数据,得:△t1=2×10-3s
△t2=1×10-3s
所以:t2=
-△t1=3×10-3-2×10-3=1×10-3s
(3)再经△t3=2×10-3s微粒向左匀加速运动,其位移为s3=
a2△
=0.4m
粒子再经△t4微粒减速运动S4碰到B板.s4=2l-S3=0.2m
由运动学公式:s4=a2△t3?△t4-
a1
代入数据,得:△t4=(4-2
)×10-3s=0.54×10-3s.
故微粒运动到B板的总时间t=△t1+△t2+△t3+△t4=5.54×10-3s
答:(1)在t=0时刻从静止出发的微粒,会在
×10-3s时刻到达A极板.
(2)若在t=0到t=
这段时间内的某一时刻t2产生的微粒刚好不能到达A板,则t2=1×10-3s.
(3)t2时刻产生的微粒到达B板所需的时间为5.54×10-3s.
 解:
解:(1)当电压为U0时,微粒的加速度a1=
| U0q |
| 2lm |
微粒向A板做匀加速运动,位移l=
| 1 |
| 2 |
| t | 2 1 |
解得t1=
| 6 |
| T |
| 2 |
所以在t=0时刻从静止出发的微粒,会在
| 6 |
(2)当电压为2U0时,微粒的加速度a2=
| 2U0q |
| 2lm |
微粒先经△t1时间加速,再经△t2时间恰好到达A板,速度减为零.位移分别为S1、S2
加速的位移s1=
| 1 |
| 2 |
| t | 2 1 |
减速的加速度为加速的加速度的2倍,所以减速的位移s2=
| 1 |
| 2 |
加速的末速度等于减速的初速度,所以a2△t=a1△t1
又因为l=S1+S2
代入数据,得:△t1=2×10-3s
△t2=1×10-3s
所以:t2=
| T |
| 2 |
(3)再经△t3=2×10-3s微粒向左匀加速运动,其位移为s3=
| 1 |
| 2 |
| t | 2 3 |
粒子再经△t4微粒减速运动S4碰到B板.s4=2l-S3=0.2m
由运动学公式:s4=a2△t3?△t4-
| 1 |
| 2 |
| t | 2 4 |
代入数据,得:△t4=(4-2
| 3 |
故微粒运动到B板的总时间t=△t1+△t2+△t3+△t4=5.54×10-3s
答:(1)在t=0时刻从静止出发的微粒,会在
| 6 |
(2)若在t=0到t=
| T |
| 2 |
(3)t2时刻产生的微粒到达B板所需的时间为5.54×10-3s.
点评:解决本题的关键理清粒子的运动规律,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
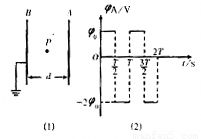
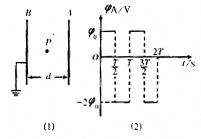 如图(1)中A和B是真空中的两块面积很大的平行金属板,加上周期为T的交流电压,在两板间产生交变的匀强电场.已知B板电势为零,A板电势φA随时间t变化的规律如图(2)所示,其中φA的最大值为φ0,最小值为-2φ0.两板间距为d,在两板之间的中点P处,不断地产生电荷为q、质量为m的带负电粒子(不计重力),这种粒子产生后,从静止出发在电场力的作用下运动.设粒子一旦碰到金属板,它就附着在板上不再运动,且其电荷量同时消失,不影响A、B板的电势.已知上述的T、φ0、d、q和m等各量的值正好满足d2=
如图(1)中A和B是真空中的两块面积很大的平行金属板,加上周期为T的交流电压,在两板间产生交变的匀强电场.已知B板电势为零,A板电势φA随时间t变化的规律如图(2)所示,其中φA的最大值为φ0,最小值为-2φ0.两板间距为d,在两板之间的中点P处,不断地产生电荷为q、质量为m的带负电粒子(不计重力),这种粒子产生后,从静止出发在电场力的作用下运动.设粒子一旦碰到金属板,它就附着在板上不再运动,且其电荷量同时消失,不影响A、B板的电势.已知上述的T、φ0、d、q和m等各量的值正好满足d2=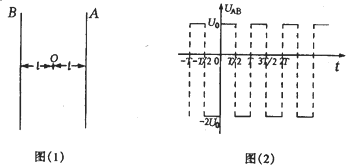 (2006?徐州一模)在图(l)中 A和B是真空中的两块面积很大的平行金属板,A、B间的电压 UAB随时间变化的规律如图(2)所示,在图(1)中O点到A和B的距离皆为l,在O处不断地产生电荷量为q、质量为m的带负电的微粒,在交变电压变化的每个周期T内,均匀产生300个上述微粒,不计重力,不考虑微粒之间的相互作用,这种微粒产生后,从静止出发在电场力的作用下运动,设微粒一旦碰到金属板,它就附在板上不再运动.且其电量同时消失,不影响A、B板的电势.已知上述的T=1.2×10-2s.U0=1.2×103 V,微粒电荷量q=10-7C,质量m=5×10-10kg,l=0.6m.
(2006?徐州一模)在图(l)中 A和B是真空中的两块面积很大的平行金属板,A、B间的电压 UAB随时间变化的规律如图(2)所示,在图(1)中O点到A和B的距离皆为l,在O处不断地产生电荷量为q、质量为m的带负电的微粒,在交变电压变化的每个周期T内,均匀产生300个上述微粒,不计重力,不考虑微粒之间的相互作用,这种微粒产生后,从静止出发在电场力的作用下运动,设微粒一旦碰到金属板,它就附在板上不再运动.且其电量同时消失,不影响A、B板的电势.已知上述的T=1.2×10-2s.U0=1.2×103 V,微粒电荷量q=10-7C,质量m=5×10-10kg,l=0.6m.
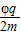
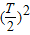 ,设求在t=0到
,设求在t=0到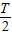 的这段时间内产生的粒子中哪一段时间内的粒子可打在A板上?
的这段时间内产生的粒子中哪一段时间内的粒子可打在A板上?