题目内容
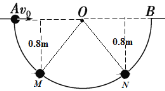
【题目】用如图甲所示的装置来验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系：
(1)实验中,直接测定小球碰撞前后的速度是不容易的,但是,可以通过仅测量______填选项前的序号),间接地解决这个问题；
A.小球开始释放高度h B.小球抛出点距地面的高度H C.小球做平抛运动的射程
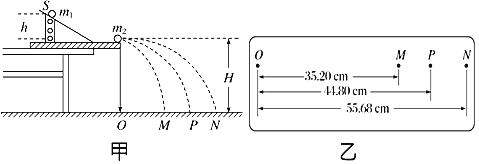
(2)图甲中O点是小球抛出点在地面上的垂直投影,实验时,先让入射球m1多次从斜轨上S位置静止释放，找到其平均落地点的位置P.测量平抛射程,把被碰小球m2静止于轨道的水平部分,再将入射小球m1从斜轨上S位置静释放,与小球m2相撞,并多次重复。
接下来要完成的必要步骤是_____________(填选项的符号)
A用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h；
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N；
E.测量平抛射程OM、ON.
(3)若两球相碰前后的动量守恒,其表达式可表示为_____________(用②中测量的量表示)；若碰撞是弹性碰撞,那么还应满足的表达式为_______________(用②中测量的量表示).
(4)经测定, m1=45.0g，m2=75.0g,小球落地点的平均位置距O点的距离如图乙所示，碰撞前m1的动量分别为P1与P1＇，则P1:P1=______________；若碰撞结束时m2的动量为P2＇，则P1＇:P2＇=11：_______，实验结果说明,碰撞前、后总动量的比值
为___________.
【答案】C ADE 
1.01
【解析】
验证动量守恒定律实验中，质量可测而瞬时速度较难．因此采用了落地高度不变的情况下，水平射程来反映平抛的初速度大小，所以仅测量小球抛出的水平射程来间接测出速度；过程中小球释放高度不需要，小球抛出高度也不要求．最后可通过质量与水平射程乘积来验证动量是否守恒；根据碰撞前后动量守恒可以写成表达式，若碰撞为弹性碰撞，则碰撞前后动能相同；根据表达式将数据代入即可求出比值。
解：(1)验证动量守恒定律实验中，即研究两个小球在轨道水平部分碰撞前后的动量关系，直接测定小球碰撞前后的速度是不容易的，根据平抛运动规律，若落地高度不变，则运动时间不变，因此可以用水平射程大小来体现速度速度大小，故需要测量水平射程，故A、B错误，C正确；
故选C；
(2)碰撞过程中动量、能量均守恒，因此有：
，
， 因此有：
，因此要使入射小球m1碰后不被反弹，应该满足m1>m2；实验时，先让入射球ml多次从斜轨上S位置静止释放，找到其平均落地点的位置P，测量平抛射程OP，然后把被碰小球m2静置于轨道的水平部分，再将入射球ml从斜轨上S位置静止释放，与小球m2相碰，并多次重复；测量平均落点的位置，找到平抛运动的水平位移，因此步骤中D、E是必须的，而且D要在E之前，至于用天平秤质量先后均可以，故选ADE；
(3)根据平抛运动可知，落地高度相同，则运动时间相同，设落地时间为t，则：
，
， 
， 而动量守恒的表达式是：，若两球相碰前后的动量守恒，则需要验证表达式
即可；
若为弹性碰撞，则碰撞前后系统动能相同，则有：，将即满足关系式：
(4)碰撞前后m1动量之比：
， 
，说明碰撞前、后总动量的比值
