题目内容
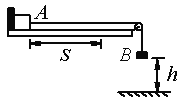
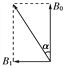
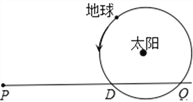
【题目】如图所示，地球质量为M，绕太阳做匀速圆周运动，半径为R。有一质量为m的飞船，由静止开始从P点在恒力F的作用下，沿PD方向做匀加速直线运动，一年后在D点飞船掠过地球上空，再过三个月，又在Q处掠过地球上空。根据以上条件可以得出
A. DQ的距离为
B. PD的距离为
C. 地球与太阳的万有引力的大小
D. 地球与太阳的万有引力的大小
【答案】ABC
【解析】试题分析：根据DQ的时间与周期的关系得出D到Q所走的圆心角，结合几何关系求出DQ的距离．抓住飞船做匀加速直线运动，结合PD的时间和PQ的时间之比得出位移之比，从而得出PD的距离．根据位移时间公式和牛顿第二定律，结合地球与太阳之间的引力等于地球的向心力求出引力的大小．
地球绕太阳运动的周期为一年，飞船从D到Q所用的时间为三个月，则地球从D到Q的时间为三个月，即四分之一个周期，转动的角度为90度，根据几何关系知，DQ的距离为
，故A正确；因为P到D的时间为一年，D到Q的时间为三个月，可知P到D的时间和P到Q的时间之比为4：5，根据
得，PD和PQ距离之比为16：25，则PD和DQ的距离之比为16：9， 
，则
，B正确；地球与太阳的万有引力等于地球做圆周运动的向心力，对PD段，根据位移公式有： 
，因为P到D的时间和D到Q的时间之比为4：1，则
，即T=t，向心力
，联立解得地球与太阳之间的引力
，故C正确D错误．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
