题目内容
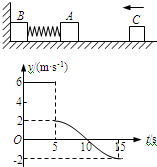 (2006?东城区三模)如图所示,物体A、B的质量分别是4kg和8kg,由轻弹簧相连接,放在光滑的水平面上,物体B左端与竖直墙壁相接触,另有一个物体C水平向左运动,在t=5s时与物体A相碰,并立即与A有相同的速度,一起向左运动.物体C的速度-时间图象如图所示.
(2006?东城区三模)如图所示,物体A、B的质量分别是4kg和8kg,由轻弹簧相连接,放在光滑的水平面上,物体B左端与竖直墙壁相接触,另有一个物体C水平向左运动,在t=5s时与物体A相碰,并立即与A有相同的速度,一起向左运动.物体C的速度-时间图象如图所示.(1)求物体C的质量.
(2)弹簧压缩具有的最大弹性势能.
(3)在5s到10s的时间内墙壁对物体B的作用力的功.
(4)在5s到15s的时间内墙壁对物体B的作用力的冲量.
分析:(1)AC碰撞过程动量守恒,由动量守恒定律可以求出C的质量.
(2)由能量守恒定律可以求出弹簧的最大弹性势能.
(3)根据做功的条件分析答题.
(4)由动量定理分析答题.
(2)由能量守恒定律可以求出弹簧的最大弹性势能.
(3)根据做功的条件分析答题.
(4)由动量定理分析答题.
解答:解:(1)由图象可知,碰前C的速度v0=6m/s,碰后的速度v=2m/s,
A、C碰撞过程动量守恒,由动量守恒定律得:mCv0=(mC+mA)v,解得mC=2kg;
(2)A、B、C向左运动,当它们速度变为零时,弹簧压缩量最大,弹簧的弹性势能最大,
由能量守恒定律得,最大弹性势能EP=
=(mC+mA)v2=12J;
(3)在5s到10s的时间内B物体的位移为零,则墙壁对物体B的作用力的功为零.
(4)由图象可知,在15s时,C的速度为v′-2m/s,
此时弹簧恢复原长,A、C的速度相等,而B的速度仍然为零,
在5s到15s内,对A、B、C三者组成的系统,由动量定理,得:
墙壁对B的冲量I=(mC+mA)v′-(mC+mA)v=(2+4)×(-2)-(2+4)×2=-24N?s,负号表示方向向右.
答:(1)物体C的质量为2kg.
(2)弹簧压缩具有的最大弹性势能为12J.
(3)在5s到10s的时间内墙壁对物体B的作用力的功为零.
(4)在5s到15s的时间内墙壁对物体B的作用力的冲量大小为24N?s,方向向右.
A、C碰撞过程动量守恒,由动量守恒定律得:mCv0=(mC+mA)v,解得mC=2kg;
(2)A、B、C向左运动,当它们速度变为零时,弹簧压缩量最大,弹簧的弹性势能最大,
由能量守恒定律得,最大弹性势能EP=
| 1 |
| 2 |
(3)在5s到10s的时间内B物体的位移为零,则墙壁对物体B的作用力的功为零.
(4)由图象可知,在15s时,C的速度为v′-2m/s,
此时弹簧恢复原长,A、C的速度相等,而B的速度仍然为零,
在5s到15s内,对A、B、C三者组成的系统,由动量定理,得:
墙壁对B的冲量I=(mC+mA)v′-(mC+mA)v=(2+4)×(-2)-(2+4)×2=-24N?s,负号表示方向向右.
答:(1)物体C的质量为2kg.
(2)弹簧压缩具有的最大弹性势能为12J.
(3)在5s到10s的时间内墙壁对物体B的作用力的功为零.
(4)在5s到15s的时间内墙壁对物体B的作用力的冲量大小为24N?s,方向向右.
点评:分析清楚物体的运动过程、正确选择研究对象是正确解题的关键,应用动量守恒定律、能量守恒定律、动量定理即可正确解题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (2006?东城区三模)电子所带电荷量最早是由美国科学家密立根所做的油滴实验测得的.密立根油滴实验的原理如图所示,两块水平放置的平行金属板与电源相连接,使上板带正电,下板带负电,油滴从喷雾器喷出后,经过上面金属板中间的小孔,落到两板之间的匀强电场中,在强光照射下,观察者通过显微镜观察油滴的运动.大多数油滴在经过喷雾器喷嘴时因摩擦而带电,密立根通过实验测得数千个油滴所带电荷量,并分析得出这些电荷量都等于某个最小电荷量的整数倍,这个最小电荷量即电子所带电荷量.
(2006?东城区三模)电子所带电荷量最早是由美国科学家密立根所做的油滴实验测得的.密立根油滴实验的原理如图所示,两块水平放置的平行金属板与电源相连接,使上板带正电,下板带负电,油滴从喷雾器喷出后,经过上面金属板中间的小孔,落到两板之间的匀强电场中,在强光照射下,观察者通过显微镜观察油滴的运动.大多数油滴在经过喷雾器喷嘴时因摩擦而带电,密立根通过实验测得数千个油滴所带电荷量,并分析得出这些电荷量都等于某个最小电荷量的整数倍,这个最小电荷量即电子所带电荷量.