题目内容
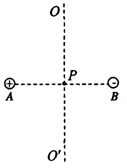
如图所示,质量为m的物体用细绳经过光滑小孔牵引在光滑水平面上做匀速圆周运动,拉力为某个值F时,转动半径为R,当拉力逐渐减小到 时,物体以另一线速度仍做匀速圆周运动,半径为2R,则物体克服外力所做的功是( )
时,物体以另一线速度仍做匀速圆周运动,半径为2R,则物体克服外力所做的功是( )
| A.0 | B. | C. | D. |
B
解析试题分析:设物体两次做匀速圆周运动的速度分别为v1和v2,根据牛顿第二定律可知,当拉力为F时有:F=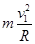 ①
①
当拉力为 时有:
时有: =
=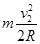 ②
②
物体在整个运动过程中受重力mg、水平面的支持力N和拉力作用,由于mg和N在竖直方向上,与速度方向始终垂直,因此始终不做功,根据动能定理有:WF= -
- ③
③
W克=-WF ④
由①②③④式联立解得:W克= ,故选项B正确。
,故选项B正确。
考点:本题主要考查牛顿第二定律和动能定理的应用问题,属于中档题。

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案如图所示,在倾角为300的足够长的光滑的斜面上有一质量为m的物体,它受到沿斜面方向的力F的作用。力F可按图(a)、(b)(c)、(d)所示的四种方式随时间变化(图中纵坐标是F与mg的比值,力沿斜面向上为正)。已知此物体在t=0时速度为零,若用v1、v2、v3、v4分别表示上述四种受力情况下物体在3秒末的速率,则这四个速率中最大的是( )
| A.v1 | B.v2 | C.v3 | D.v4 |
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成 角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成
角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成 角,若
角,若 ,则下列说法正确的是( )
,则下列说法正确的是( )
| A.轻杆对小球的弹力方向与细线平行 |
| B.轻杆对小球的弹力方向沿着轻杆方向向上 |
| C.轻杆对小球的弹力方向既不与细线平行也不沿着轻杆方向 |
| D.此时轻杆的形变包括拉伸形变与弯曲形变 |
如图所示,轻弹簧上端固定在O点,下端连接一个小球,小球静止在N位置,P位置是弹簧原长处.现用力将物块竖直向下拉至Q处释放,物块能上升的最高处在P位置上方。设弹簧的形变始终未超过弹性限度,不计空气阻力,在物块上升过程,下列判断正确的是
| A.在Q处,小球的加速度小于g |
| B.从Q到N的过程,小球的加速度不断增大 |
| C.在N处,小球的速度最大 |
| D.从N到P的过程,小球机械能守恒 |
关于做曲线运动的物体,下列说法正确的是
| A.物体所受合力一定为零 | B.物体所受合力一定不变 |
| C.物体的加速度不为零 | D.物体的加速度与速度不在一条直线上 |