题目内容
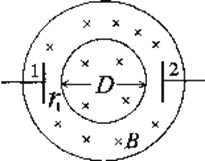
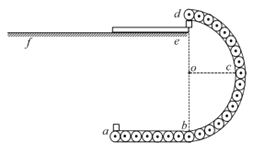
【题目】某传送带装置在竖直平面内的横截面如图所示，ab 段水平，bcd 段为1/2 圆周．传送带在电机的带动下以恒定速率ν = 4m/s 运动，在传送带的左端点a 无初速地投放质量m=1kg 的小物块（可视为质点），当第一个物块A 到达b 点时即刻在a 点投放另一相同的物块 B．物块到达b 点时都恰好与传送带等速，此后能确保物块与传送带相对静止地通过bcd 段．物块到达最高点d 时与传送带间的弹力大小恰等于其重力．在d 端点的左方另有一平直轨道ef，轨道上静止停放着质量M=1kg 的木板，从d 点出来的物块恰能水平进入木板上表面的最右端，木板足够长．已知：物块与传送带间的动摩擦因数
= 0.8 ，与木板间的动摩擦因数
=0.2 ；木板与轨道间的动摩擦因数
=0.1；设最大静摩擦力等于滑动摩擦力，取g=10m/s2．试求：
（1）每个物块在传送带abcd 上运行的时间；
（2）传输A 物块，电机所需提供的能量（不计传动机构的其他能量损耗）；
（3）木板运动的总时间．
【答案】(1)1.13s (2)32J (3) 
【解析】(1)物块在
上做匀加速直线运动，根据牛顿第二定律
得： 
，得
m/s2 ①
得
s ②
物块经过
点时根据牛顿第二定律得：
，代入
，得
m ③
则物块在圆周上运动的时间： 
s ④
则每个物块在传送带上运动的时间
s ⑤
(2)物块在传送带上加速时与传送带间的相对位移
m ⑥
每传输一个物块，电机提供的能量
J ⑦
[或：物块在传送带水平
段运动，电机克服摩擦力做功
⑥ 
每传输一个物块，电机提供的能量
J ⑦ ]
(3) 
物块滑上木板时，物块与木板间的滑动摩擦力大小
⑧
木板与轨道间的最大静摩擦力大小
⑨
由于
，故木板仍保持静止状态 ⑩
物块
在木板上做减速运动，其加速度大小： 
当
物块滑上木板瞬间， 
物块的速度大小： 
m/s
物块在木板上同时滑动时对木板的摩擦力大小为
地面与木板间的最大静摩擦力
木板开始加速向左运动，由牛顿第二定律： 
得： 
m/s2
当
物块与木板共速时有： 
得： 
m/s， 
s （
此时，物块
的速度大小. 
m/s
此后
物块与木板保持相对静止，木板开始减速，由牛顿第二定律：
得： 
m/s2
设物块
与木板达到共速后，再减速停下，则有：
得： 
， 
m/s假设成立 
此后三个物体一起做减速运动： 
m/s2 
三个体一起减速运动的时间： 
s 
木板运动的总时间： 
s 
方法二： 
图像法
作图需有相应的计算表达式。参照前一种解法，分阶段对应给分。
