题目内容
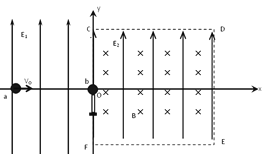
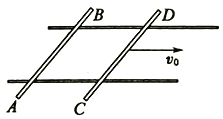
【题目】如图所示，在竖直向上磁感应强度为
匀强磁场中，两条足够长光滑平行金属导轨固定在水平桌面上，间距
，电阻不计，匀强磁场方向与导轨平面垂直，金属棒AB、CD水平放在两导轨上，相隔为
，棒与导轨垂直并保持良好接触，AB棒质量为
，CD棒质量为
，两金属棒接入电路的总电阻
，若CD棒以
的初速度水平向右运动，在两根金属棒运动到两棒间距最大的过程中，下列说法正确的是
A. AB棒的最终速度大小为
B. 该过程中电路中产生的热量为
C. 该过程中通过导体横截面的电荷量为
D. 两金属板的最大距离为
【答案】BC
【解析】
金属导轨光滑，两金属棒组成的系统所受合外力为零，系统动量守恒，由动量守恒定律可以求出棒的最终速度；由能量守恒定律可以求出电路产生的热量，应用动量定理可以求出通过导体横截面的电荷量，然后求出两金属棒的最大距离。
A、开始CD棒做减速运动、AB棒做加速运动，当两者速度相等时它们间的距离最大，两棒组成的系统动量守恒，以向右为正方向，由动量守恒定律得：
，解得：
，故A错误；
B、对系统，由能量守恒定律得：
，解得：
，故B正确；
C、对AB棒，由动量定理得：
，而：
，则：
，解得：
，故C正确；
D、通过导体横截面的电荷量：
，两金属棒间的最大距离：
，故D错误；
故选BC.
练习册系列答案
相关题目
