题目内容
 某静止放射性元素的原子核在磁感应强度B=2.5T的匀强磁场中发生衰变,轨迹如图所示,测得两圆的半径之比R1:R2=42:1,且R1=0.2m.已知α粒子质量mα=6.64×10-27 kg,β粒子质量mβ=9.1×10-31 kg.
某静止放射性元素的原子核在磁感应强度B=2.5T的匀强磁场中发生衰变,轨迹如图所示,测得两圆的半径之比R1:R2=42:1,且R1=0.2m.已知α粒子质量mα=6.64×10-27 kg,β粒子质量mβ=9.1×10-31 kg.(1)判断发生的是何种衰变;
(2)判断衰变前原子核的种类;
(3)求出放出粒子的速度大小.
分析:(1)通过轨迹圆外切,结合速度的方向和洛伦兹力的方向判断出粒子的带电性质,从而判断出是何种衰变.
(2)结合洛伦兹力提供向心力,通过半径公式,动量守恒定律求出衰变后的粒子电荷的比值,从而确定衰变前原子核的电荷数,得出原子核的种类.
(3)结合半径公式,求出放出粒子的速度大小.
(2)结合洛伦兹力提供向心力,通过半径公式,动量守恒定律求出衰变后的粒子电荷的比值,从而确定衰变前原子核的电荷数,得出原子核的种类.
(3)结合半径公式,求出放出粒子的速度大小.
解答:解:(1)衰变过程中动量守恒,因初动量为零,故衰变后两粒子动量大小相等,方向相反.粒子轨迹为外切圆,说明两粒子所受的洛伦兹力方向相反,均带正电,故发生的是α衰变.
(2)由动量守恒0=mv-mαvα,粒子做圆周运动向心力等于洛伦兹力qvB=
,
又qα=2e,R1?:R2=42?:1,由以上关系得该放射性元素的电荷量q=84e,即衰变前原子核的电荷数为86,是氡核.
(3)因R1=
,得
vα=
=
m/s≈2.4×107 m/s.
答:(1)该衰变为α衰变
(2)衰变前原子核为氡核
(3)放出粒子的速度大小为2.4×107 m/s.
(2)由动量守恒0=mv-mαvα,粒子做圆周运动向心力等于洛伦兹力qvB=
| mv2 |
| r |
又qα=2e,R1?:R2=42?:1,由以上关系得该放射性元素的电荷量q=84e,即衰变前原子核的电荷数为86,是氡核.
(3)因R1=
| mαvα |
| qαB |
vα=
| qαBR1 |
| mα |
| 2×1.6×10-19×2.5×0.2 |
| 6.64×10-27 |
答:(1)该衰变为α衰变
(2)衰变前原子核为氡核
(3)放出粒子的速度大小为2.4×107 m/s.
点评:本题考查了动量守恒定律、粒子在磁场中做圆周运动的半径公式等知识点,难度中等,综合性较强,需加强这方面的训练.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 的油酸酒精溶液逐滴滴入量筒,记下
的油酸酒精溶液逐滴滴入量筒,记下 。
。 (3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将
(3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将 (2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是
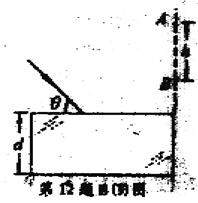
(2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是 (3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针
(3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针 (1)下列说法中正确的是___▲_____
(1)下列说法中正确的是___▲_____  (3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端
(3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端 的内容及实验步骤
的内容及实验步骤 中的计算式:
中的计算式: 的油酸酒精溶液逐滴滴入量筒,记下
的油酸酒精溶液逐滴滴入量筒,记下 的油酸酒精溶液的滴数
的油酸酒精溶液的滴数 ;
; ;
; 的正方形为单位,计算轮廓内正方形的个数
的正方形为单位,计算轮廓内正方形的个数 ;
; __▲____
__▲____ 。
。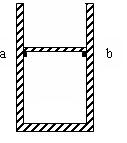 (3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将
(3)如图所示,上端开口的光滑圆柱形气缸竖直放置,截面积为40cm2的活塞将 (2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是
(2)(4分)如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图像,屏上每一小格长度为1cm。在t=0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播)。此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是 (3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针
(3)(4分)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针 、
、 确定入射光线,并让入射光线过圆心
确定入射光线,并让入射光线过圆心 ,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针
,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针 ,使
,使 。图中
。图中 为分界面,虚线半圆与玻璃砖对称,
为分界面,虚线半圆与玻璃砖对称, 、
、 、
、 均垂直于法线并分别交法线于
均垂直于法线并分别交法线于 、
、 点。设
点。设 ,
, 的长度为
的长度为 ,
, ,
, 的长度为
的长度为 ,求:
,求: (1)下列说法中正确的是___▲_____
(1)下列说法中正确的是___▲_____  (3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端
(3)如图,质量为m的小球系于长L=0.8m的轻绳末端。绳的另一端