题目内容
如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求:
(1)两板间电场强度E;
(2)第4个小球刚要离开电场时杆的速度;
(3)从第2个小球刚进入电场开始计时,到第4个小球刚要离开电场所用的时间.
(1)两板间电场强度E;
(2)第4个小球刚要离开电场时杆的速度;
(3)从第2个小球刚进入电场开始计时,到第4个小球刚要离开电场所用的时间.

(1)从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,受力平衡,则有:
2qE=4mg,
E=
,
(2)从静止开始到第4个小球刚要离开电场得过程中运用动能定理得:
4mg×5L-4qE×2L=
×4mv2
解得:v=
,
(3)设杆匀速运动时速度为v1,对第1个小球刚进入电场到第3个小球刚要进入电场这个过程,应用动能定理得:
4mg×2L-qE(L+2L)=
×4mv12
解得:v1=
第2个小球刚进入电场到第3个小球刚要离开电场这段时间,整个杆做匀速直线运动,设运动时间为t1,则:
t1=
=
第3个小球离开电场后,只有第4个小球在电场中,杆做匀加速直线运动,设运动时间为t2,则:
t2=
=
所以总时间为:t=t1+t2=
答:(1)两板间电场强度E为
;
(2)第4个小球刚要离开电场时杆的速度为
;
(3)从第2个小球刚进入电场开始计时,到第4个小球刚要离开电场所用的时间为
.
2qE=4mg,
E=
| 2mg |
| q |
(2)从静止开始到第4个小球刚要离开电场得过程中运用动能定理得:
4mg×5L-4qE×2L=
| 1 |
| 2 |
解得:v=
| 2gL |
(3)设杆匀速运动时速度为v1,对第1个小球刚进入电场到第3个小球刚要进入电场这个过程,应用动能定理得:
4mg×2L-qE(L+2L)=
| 1 |
| 2 |
解得:v1=
| gL |
第2个小球刚进入电场到第3个小球刚要离开电场这段时间,整个杆做匀速直线运动,设运动时间为t1,则:
t1=
| 3L |
| v1 |
3
| ||
| g |
第3个小球离开电场后,只有第4个小球在电场中,杆做匀加速直线运动,设运动时间为t2,则:
t2=
| L | ||
|
2(
| ||||
| g |
所以总时间为:t=t1+t2=
(2
| ||||
| g |
答:(1)两板间电场强度E为
| 2mg |
| q |
(2)第4个小球刚要离开电场时杆的速度为
| 2gl |
(3)从第2个小球刚进入电场开始计时,到第4个小球刚要离开电场所用的时间为
(2
| ||||
| g |

练习册系列答案
相关题目
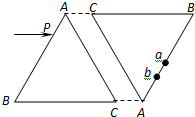 如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后从a、b两点射出.对于从a、b射出的这两束光下列说法中正确的( )
如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后从a、b两点射出.对于从a、b射出的这两束光下列说法中正确的( )| A、在玻璃中,从a点射出光的传播速度比从b点射出光的传播速度大 | B、从a点射出的为蓝光,从b点射出的为红光 | C、从a、b两点射出的两束光仍平行,且平行于BC | D、从a、b两点射出的两束光不平行 |
 (2010?江西模拟)如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中.两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后变为从a、b两点射出的单色光.对于这两束单色光,下列判断正确的是( )
(2010?江西模拟)如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中.两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后变为从a、b两点射出的单色光.对于这两束单色光,下列判断正确的是( ) (2009?广州二模)如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求:
(2009?广州二模)如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求: 如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d.且L>d,上极板的电势比下极板高U.质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出.不计离子重力及离子间相互作用的影响.
如图所示,两块相同的金属板正对着水平放置,金属板长为L,两板间距离为d.且L>d,上极板的电势比下极板高U.质量为m、带电量为q的正离子束,沿两板间中心轴线以初速度υ0进入两板间,最终都能从两板间射出.不计离子重力及离子间相互作用的影响.