题目内容
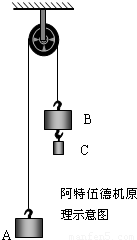
 如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,缂子不可伸长,如果m=
如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,缂子不可伸长,如果m=| 1 | 4 |
(1)物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值;
(2)系统由静止释放后运动过程中物体C对B的拉力.
分析:(1)隔离A,对B、C整体分析,运用牛顿第二定律求出加速度的大小,结合位移时间公式求出物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值.
(2)隔离对C分析,运用牛顿第二定律求出拉力的大小.
(2)隔离对C分析,运用牛顿第二定律求出拉力的大小.
解答:解:(1)设物体的加速度为a,绳子的张力为T,
对物体A:T-Mg=Ma
对B、C整体:(M+m)g-T=(M+m)a
解得a=
g.
因为m=
M
所以a=
g=
g
根据运动学公式得,h=
at2,h=
gt02
解得
=
=3
所以物体B从静止开始下落一段距离的时间是自由下落同样距离所用时间的3倍.
(2)设B、C间的拉力为F,
对C物体:mg-F=ma
F=mg-ma=
mg
由牛顿第三定律知,C对B的拉力为
mg.
答:(1)物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值为3.(2)系统由静止释放后运动过程中物体C对B的拉力为
mg.
对物体A:T-Mg=Ma
对B、C整体:(M+m)g-T=(M+m)a
解得a=
| m |
| 2M+m |
因为m=
| 1 |
| 4 |
所以a=
| m |
| 2M+m |
| 1 |
| 9 |
根据运动学公式得,h=
| 1 |
| 2 |
| 1 |
| 2 |
解得
| t |
| t0 |
|
所以物体B从静止开始下落一段距离的时间是自由下落同样距离所用时间的3倍.
(2)设B、C间的拉力为F,
对C物体:mg-F=ma
F=mg-ma=
| 8 |
| 9 |
由牛顿第三定律知,C对B的拉力为
| 8 |
| 9 |
答:(1)物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值为3.(2)系统由静止释放后运动过程中物体C对B的拉力为
| 8 |
| 9 |
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,掌握整体法和隔离法的运用.

练习册系列答案
相关题目
 如图所示的装置叫做阿特伍德机,是阿特伍德(G.Atwood1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究.已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,绳子不可伸长,如果
如图所示的装置叫做阿特伍德机,是阿特伍德(G.Atwood1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究.已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,绳子不可伸长,如果
 ,求:
,求:
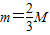 ,求
,求