题目内容
【题目】如图（a）所示，A、B为钉在光滑水平面上的两根铁钉，质量为0.6kg的小球C（小球可视为质点）用细绳拴在铁钉B上，A、B、C在同一直线上．t=0时，给小球一垂直于绳，大小为2m/s的速度，使小球在水平面上做圆周运动．在0≤t≤t2时间内，细绳的拉力随时间变化的规律如图（b）所示．若细绳能承受的最大拉力为6.4N，则下列说法中正确的是（）
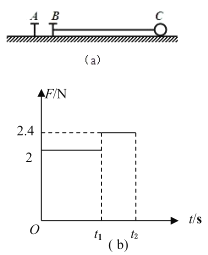
A. 两钉子间的距离为0.2m
B. t=3.3s时细绳拉力的为3N
C. t1为0.6πs
D. 小球从开始运动到绳被拉断历时2πs
【答案】ACD
【解析】
A.由牛顿第二定律可得：
，当F=2N时，r1=1. 2m，F=2. 4N时，r2=1m，两钉子间的距离d为小球做圆周运动减小的半径即
，故A正确；
BC.由周期
可得，r1=1. 2m时，T1=1. 2πS，r2=1m时，T2=πs，而小球每经半个周期与另一钉子接触，小球从开始运动经T1/2=0. 6πs绳子与铁钉A接触，小球做圆周运动半径减小，绳子受到的拉力增大，所以t1=0. 6π；小球从开始运动经
=3. 45s＞3. 3s绳子才再次与铁钉B接触，所以t=3. 3s时细绳拉力仍为2. 4N，故B错误，C正确；
D.当绳受到的拉力为6. 4N时，r=0. 375m＜0. 4m，即当r=0. 4m时，绳子还不会断，小球从开始运动到绳被拉断历时
，故D正确.
故选：ACD
练习册系列答案
相关题目
