题目内容
12. 如图所示,竖直平面内有一粗糙的圆弧圆管轨道,其半径为R=0.5m,内径很小.平台高h=1.9m,一质量m=0.5kg、直径略小于圆管内径的小球,从平台边缘的A处水平射出,恰能沿圆管轨道上P点的切线方向进入圆管内,轨道半径OP与竖直线的夹角为37°.g=10m/s2,sin37°=0.6,cos37°=0.8.不计空气阻力.求:
如图所示,竖直平面内有一粗糙的圆弧圆管轨道,其半径为R=0.5m,内径很小.平台高h=1.9m,一质量m=0.5kg、直径略小于圆管内径的小球,从平台边缘的A处水平射出,恰能沿圆管轨道上P点的切线方向进入圆管内,轨道半径OP与竖直线的夹角为37°.g=10m/s2,sin37°=0.6,cos37°=0.8.不计空气阻力.求:(1)小球从平台上的A点射出时的速度v0 和P点速度VP是多大?
(2)小球通过最高点Q时,小球对圆管轨道向下的压力FQ=3N,求Q点速度VQ多大?
分析 (1)小球离开平台之后做的是平抛运动,小球恰能沿圆管轨道上P点的切线方向进入圆管内,说明末速度的方向就沿圆管的切线方向;
(2)小球在圆管内做的是圆周运动,根据再最高点的受力的情况,可以求得速度的大小.
解答 解:(1)设小球抛出后做平抛运动至P,竖直位移为:y=h-R(1-cos37°)
由 y=$\frac{1}{2}$gt2知平抛用时为:
t=$\sqrt{\frac{2y}{g}}$=0.6s
小球达P点竖直速度小球达P点竖直速度为:vy=gt=6m/s
小球恰沿P点切线方向进入圆管,由速度关系:
tanθ=$\frac{{v}_{y}}{{v}_{0}}$,
小球从平台上的A点射出时的速度为:v0=$\frac{{v}_{y}}{tan37°}$=8m/s
小球在P点速度为:vp=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=10m/s$
(2)小球在圆周Q点,由牛顿第二定律:
mg-FQ=m$\frac{{{v}_{Q}}^{2}}{R}$
解得:${v}_{Q}=\sqrt{2}m/s$
答:(1)小球从平台上的A点射出时的速度v0 为8m/s,P点速度VP是10m/s;
(2)小球通过最高点Q时,小球对圆管轨道向下的压力FQ=3N,Q点速度VQ为$\sqrt{2}m/s$.
点评 恰能无碰撞地沿圆弧切线从P点进入光滑竖直圆弧轨道,这是解这道题的关键,理解了这句话就可以求得小球的末速度,本题很好的把平抛运动和圆周运动结合在一起,能够很好的考查学生的能力,是道好题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
3.关于自由落体运动,下列说法中不正确的是( )
| A. | 自由落体运动是竖直方向的匀加速直线运动 | |
| B. | 前1s、前2s、前3s竖直方向的位移之比为1:4:9的运动一定是自由落体运动 | |
| C. | 自由落体运动在开始的连续三个2s内的位移之比是1:3:5 | |
| D. | 自由落体运动在开始的连续三个2s末的速度之比是1:2:3 |
20.甲乙两个做匀速圆周运动的质点,它们的角速度之比为3:1,线速度之比为2:3,质量之比为1:1,那么下列说法中正确的是( )
| A. | 它们的半径之比是2:3 | B. | 它们的向心加速度之比为2:1 | ||
| C. | 它们的周期之比为3:1 | D. | 它们的向心力之比为1:2 |
17.如图所示的a、b、c、d中,质量为M的物体甲受到相同的恒力F的作用,在力F作用下使物体甲在水平方向移动相同的位移.μ表示物体甲与水平面间的动摩擦因数,乙是随物体甲一起运动的小物块,比较物体甲移动的过程中力F对甲所做的功的大小( )


| A. | Wa最小 | B. | Wd最大 | C. | Wa=Wc | D. | 四种情况一样大 |
4.利用下列哪组数据,可以计算出地球质量( )
| A. | 已知地球半径和地面重力加速度 | |
| B. | 已知卫星绕地球作匀速圆周运动的轨道半径和周期 | |
| C. | 已知月球绕地球作匀速圆周运动的周期和月球质量 | |
| D. | 已知同步卫星离地面高度和地球自转周期 |
1. 图中T是绕有两组线圈的闭合铁心,线圈的绕向如图所示,D是理想的二极管,金属棒ab可在两条平行的金属导轨上沿导轨滑行,磁场方向垂直纸面向里.若电流计G中有电流通过,则ab棒的运动可能是( )
图中T是绕有两组线圈的闭合铁心,线圈的绕向如图所示,D是理想的二极管,金属棒ab可在两条平行的金属导轨上沿导轨滑行,磁场方向垂直纸面向里.若电流计G中有电流通过,则ab棒的运动可能是( )
 图中T是绕有两组线圈的闭合铁心,线圈的绕向如图所示,D是理想的二极管,金属棒ab可在两条平行的金属导轨上沿导轨滑行,磁场方向垂直纸面向里.若电流计G中有电流通过,则ab棒的运动可能是( )
图中T是绕有两组线圈的闭合铁心,线圈的绕向如图所示,D是理想的二极管,金属棒ab可在两条平行的金属导轨上沿导轨滑行,磁场方向垂直纸面向里.若电流计G中有电流通过,则ab棒的运动可能是( )| A. | 向左匀速运动 | B. | 向左匀减速运动 | C. | 向右匀减速运动 | D. | 向右匀速运动 |
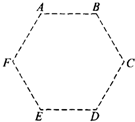 如图所示的A、B、C、D、E、F为匀强电场中正六边形的六个顶点.已知A、B、C三点的电势分别为-1V、1V、5V,则D点的电势为7V,E点的电势为5V.
如图所示的A、B、C、D、E、F为匀强电场中正六边形的六个顶点.已知A、B、C三点的电势分别为-1V、1V、5V,则D点的电势为7V,E点的电势为5V.

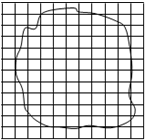 在“用油膜法估测分子的大小”的实验中,油酸酒精溶液的浓度为每104 mL溶液中有纯油酸5mL.用注射器测得1mL上述溶液有液滴100滴.把1滴该溶液滴入盛水的浅盘里,待稳定后,将玻璃板放在浅盘上描出油膜轮廓,再将玻璃板放在坐标纸上,其形状如图所示,坐标纸中正方形小方格的边长为1cm.则:
在“用油膜法估测分子的大小”的实验中,油酸酒精溶液的浓度为每104 mL溶液中有纯油酸5mL.用注射器测得1mL上述溶液有液滴100滴.把1滴该溶液滴入盛水的浅盘里,待稳定后,将玻璃板放在浅盘上描出油膜轮廓,再将玻璃板放在坐标纸上,其形状如图所示,坐标纸中正方形小方格的边长为1cm.则: