题目内容
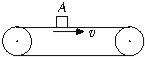
【题目】由理想电动机带动的水平传送带匀速运动,速度大小为v,现将一小工件放到传送带左端点上.设工件初速为零,当它在传送带上滑动一段距离后速度达到v而与传送带保持相对静止.设工件质量为m,它与传送带间的滑动摩擦系数为 μ,左右端相距L,则该电动机每传送完一个工件消耗的电能为( )
A. μmgL B. mv2 C. μmgL+mv2 D. mv2
【答案】D
【解析】试题分析:物体在传送带上运动时,物体和传送带要发生相对滑动,所以电动机多做的功一部分转化成了物体的动能另一部分就是增加了相同的内能.
解:在运动的过程中只有摩擦力对物体做功,由动能定理可知,摩擦力对物体做的功等于物体动能的变化,
即为:W=mv2,
根据牛顿第二定律知道工件的加速度为μg,所以速度达到v而与传送带保持相对静止所用时间:t=![]()
工件的位移为![]() ,
,
工件相对于传送带滑动的路程大小为:△x=vt﹣![]() =
=![]()
则产生的热量:Q=μmg△x=mv2
传送带克服工件对它的摩擦力做功是w,整个过程中能量守恒,根据能量守恒得:mv2+Q﹣w=0
w=mv2+Q=mv2,故D正确.
故选:D.

练习册系列答案
相关题目