题目内容
6. 一长为L的不可伸长绝缘细线的一端悬挂于O点,另一端系在质量为m,带电荷量为q的小球上,置于水平方向匀强电场中,静止时细线与竖直夹角等于30°.A、B两点分别是小球在最低位置和静止时位置.重力加速度为g.求:
一长为L的不可伸长绝缘细线的一端悬挂于O点,另一端系在质量为m,带电荷量为q的小球上,置于水平方向匀强电场中,静止时细线与竖直夹角等于30°.A、B两点分别是小球在最低位置和静止时位置.重力加速度为g.求:(1)静止时细线拉力大小;
(2)A、B两点电势差大小.
分析 (1)对小球受力分析,根据共点力的平衡条件可求得绳子拉力的大小;
(2)根据共点力的平衡求得电场力的大小,再由电场中电势差与场强间的关系可求得电势差.
解答 解:(1)由受力分析可知,在B点时小球受重力、电场力、拉力三个力处于平衡,
Tcos30°=mg
解得拉力T=$\frac{2\sqrt{3}}{3}$mg
(2)在匀强电场中,
电势差U=Ed
由几何关系 A、B两点的水平距离d=Lsin30°
由平衡可知电场力qE=$\frac{T}{2}$
或者qE=mgtan30°
联立解得电势差U=$\frac{\sqrt{3}mgL}{6q}$
答:(1)静止时细线拉力大小$\frac{2\sqrt{3}}{3}$mg
(2)A、B两点电势差大小$\frac{\sqrt{3}mgL}{6q}$.
点评 本题实质上考查了物体平衡,对于这类问题只要正确进行受力分析,然后根据平衡方程求解即可.要注意理解U=Ed的字母含义.

练习册系列答案
相关题目
9.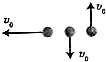 如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )
如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )
 如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )
如图所示,三个完全相同的小球在同一高度处以相同大小的初速度v0分别水平、竖直向下、竖直向上抛出.不计空气阻力,下列说法正确的是( )| A. | 小球飞行过程中单位时间内的速度变化量相同 | |
| B. | 从开始运动至落地,重力对小球做功相同 | |
| C. | 小球落地时,重力的瞬时功率均相同 | |
| D. | 从开始运动至落地,重力对小球做功的平均功率相同 |
17.在日常生活中我们使用的交流电的电压μ=220$\sqrt{2}$sin(100πt)V,下列说法中正确的是( )
| A. | 电流的方向每秒改变可50次 | |
| B. | 用电压表测其电压为220$\sqrt{2}$V | |
| C. | 标有“220V,200W”的电风扇正常工作时输出的机械功率为200W | |
| D. | 某家庭的电表处接有熔断电流为10A的保险丝,该家庭用电器消耗总功率最大值为2200W |
14.某物体在从A点运动到B点的过程中,克服重力做功为3J,拉力做功1J,克服空气阻力做功为0.5J,则在A点的( )
| A. | 重力势能比B点大3J | B. | 机械能比B点小1J | ||
| C. | 动能比B点大2.5J | D. | 机械能比B点小0.5J |
1.下列物理量中,属于标量的是( )
| A. | 向心加速度 | B. | 电势 | C. | 电场强度 | D. | 线速度 |
11.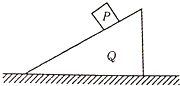 如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )
如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )
 如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )
如图,小物块P位于光滑斜面上,斜面Q位于光滑水平地面上,小物块P从静止开始沿斜面下滑的过程中( )| A. | 斜面Q静止不动 | |
| B. | 小物块P对斜面Q的弹力对斜面做正功 | |
| C. | 小物块P的机械能守恒 | |
| D. | 斜面Q对小物块P的弹力方向与接触面不垂直 |
 如图所示,让小球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好从与小球拴接处被拉断,并立即撤去摆线,小球在粗糙的水平面上由D点向D做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道,当小球进入圆轨道立即关闭A孔,已知摆线长L=2m,θ=60°,小球质量为m=0.5kg,小球与粗糙水平面动摩擦因数μ=$\frac{1}{8}$,g取10m/s2.求:
如图所示,让小球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好从与小球拴接处被拉断,并立即撤去摆线,小球在粗糙的水平面上由D点向D做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道,当小球进入圆轨道立即关闭A孔,已知摆线长L=2m,θ=60°,小球质量为m=0.5kg,小球与粗糙水平面动摩擦因数μ=$\frac{1}{8}$,g取10m/s2.求: 某学生在做“研究平抛物体运动”的实验中,得到了如图所示物体的运动轨迹.若按图示方法建立平面直角坐标系,A、B、C三点的坐标值分别如图所示,则:
某学生在做“研究平抛物体运动”的实验中,得到了如图所示物体的运动轨迹.若按图示方法建立平面直角坐标系,A、B、C三点的坐标值分别如图所示,则: 如图所示,在光滑水平桌面的两端各固定一个定滑轮,用轻绳经过滑轮将弹簧分别与质量为m1=8kg、m2=2kg的两个物体A、B相连.不计绳与滑轮之间的摩擦及弹簧秤、定滑轮的质量,g取10m/s2,弹簧秤的读数为( )
如图所示,在光滑水平桌面的两端各固定一个定滑轮,用轻绳经过滑轮将弹簧分别与质量为m1=8kg、m2=2kg的两个物体A、B相连.不计绳与滑轮之间的摩擦及弹簧秤、定滑轮的质量,g取10m/s2,弹簧秤的读数为( )