题目内容
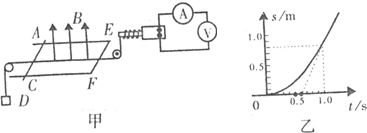
如图甲所示,不计电阻的光滑导体框架水平放置,框架中间区域有竖直向上的匀强磁场,磁感应强度为B=1T.有一导体棒AC横放在框架上,其质量为m=0.1kg,电阻为R=4Ω,现用轻绳拴住导体棒,轻绳的一端通过光滑的定滑轮绕在电动机的转轴上,另一端通过光滑的定滑轮与物体D相连.物体D的质量为M=0.3kg,电动机内阻为r=1Ω.接通电路后,电压表的读数恒为U=8V,电流表的读数恒为I=l A,电动机牵引原来静止的导体棒AC平行于时EF向右运动;其运动情况如图乙所示.(取g=10m/s2)试求:
(1)根据图乙简述金属杆的运动情况;
(2)金属棒匀速运动的速度;
(3)匀强磁场的宽度;
(4)导体棒在变速运动阶段产生的热量.
(1)根据图乙简述金属杆的运动情况;
(2)金属棒匀速运动的速度;
(3)匀强磁场的宽度;
(4)导体棒在变速运动阶段产生的热量.

分析:(1)根据图象可知,通过斜率可知运动情况,即可求解;
(2)由斜率表达速度的大小,从而即可求解;
(3)根据电动机的总功率等于内阻发热功率与输出功率,而输出功率等于重力的功率与安培力的功率之和.从而即可求解;
(4)由能量守恒定律,即可求解.
(2)由斜率表达速度的大小,从而即可求解;
(3)根据电动机的总功率等于内阻发热功率与输出功率,而输出功率等于重力的功率与安培力的功率之和.从而即可求解;
(4)由能量守恒定律,即可求解.
解答:解:(1)根据乙图可知,经过t=1秒时,杆ab移动s=1m后做匀速直线运动,
所以前1 s内导体棒做变速运动,1 s后做匀速运动,
(2)根据1秒时图线斜率可知
匀速运动速度为 v=
=2m/s
(3)根据电动机的总电功率等于重力功率与内阻发热功率及安培力功率之和,
即为,IU=Mgv+I2r+B2L2
v,
代入数据,解得:L=1 m,
(4)根据能量守恒可知,IUt=Mgh+
(M+m)v2+I2rt+Q,
解得:Q=3.8 J.
答:(1)根据图乙简述金属杆的运动情况:前1 s内导体棒做变速运动,1 s后做匀速运动;
(2)金属棒匀速运动的速度2m/s;
(3)匀强磁场的宽度1 m;
(4)导体棒在变速运动阶段产生的热量3.8 J.
所以前1 s内导体棒做变速运动,1 s后做匀速运动,
(2)根据1秒时图线斜率可知
匀速运动速度为 v=
| △s |
| △t |
(3)根据电动机的总电功率等于重力功率与内阻发热功率及安培力功率之和,
即为,IU=Mgv+I2r+B2L2
| v |
| R |
代入数据,解得:L=1 m,
(4)根据能量守恒可知,IUt=Mgh+
| 1 |
| 2 |
解得:Q=3.8 J.
答:(1)根据图乙简述金属杆的运动情况:前1 s内导体棒做变速运动,1 s后做匀速运动;
(2)金属棒匀速运动的速度2m/s;
(3)匀强磁场的宽度1 m;
(4)导体棒在变速运动阶段产生的热量3.8 J.
点评:考查图象的斜率表示的含义,掌握总功率与各消耗功率的关系,理解能量守恒定律在本题的应用.注意安培力做功与产生热量的相对应,不能重复.

练习册系列答案
相关题目
 如图甲所示,不计电阻的平行金属导轨竖直放置,导轨间距为L=l m,上端接有电阻R=3Ω,虚线OO'下方是垂直于导轨平面的匀强磁场.现将质量m=0.25kg、电阻r=1Ω的金属杆ab,从OO'上方某处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,杆下落过程中的v-t图象如图乙所示,重力加速度g取10m/s2.求:
如图甲所示,不计电阻的平行金属导轨竖直放置,导轨间距为L=l m,上端接有电阻R=3Ω,虚线OO'下方是垂直于导轨平面的匀强磁场.现将质量m=0.25kg、电阻r=1Ω的金属杆ab,从OO'上方某处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,杆下落过程中的v-t图象如图乙所示,重力加速度g取10m/s2.求:
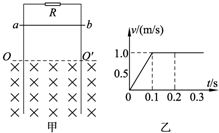 (2011?济南一模)如图甲所示,不计电阻的平行金属导轨竖直放置,导轨间距为L=1m,上端接有电阻R=3Ω,虚线OO′下方是垂直于导轨平面的匀强磁场.现将质量m=0.1kg、电阻r=1Ω的金属杆ab,从OO′上方某处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,杆下落过程中的vt图象如图乙所示.(取g=10m/s2)求:
(2011?济南一模)如图甲所示,不计电阻的平行金属导轨竖直放置,导轨间距为L=1m,上端接有电阻R=3Ω,虚线OO′下方是垂直于导轨平面的匀强磁场.现将质量m=0.1kg、电阻r=1Ω的金属杆ab,从OO′上方某处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,杆下落过程中的vt图象如图乙所示.(取g=10m/s2)求: