Question

【题目】如图甲所示，一轻质弹簧左端固定在墙壁上，右端与置于水平面上的质量为m的小滑块相连。在以下的讨论中小滑块可视为质点，弹簧始终在弹性限度内，取弹簧原长时弹性势能为0，且空气阻力可忽略不计。

（1）若水平面光滑，以弹簧原长时小滑块的位置O为坐标原点，建立水平向右的坐标轴Ox，如图甲所示。

①已知弹簧的劲度系数为k，请写出弹簧弹力F与小滑块所在位置坐标x的关系式，并借助F-x 图像确定出将小滑块由O点缓慢拉到位置坐标x的过程中，弹簧弹力所做的功。

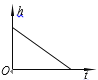
②小滑块在某轻质弹簧的作用下，沿光滑水平面在O点附近做往复运动，若从小物块向右运动通过O点时开始计时，请在图乙中定性画出小物块所受弹力F随时间t变化的关系图像；

若测得该弹簧的弹性势能Ep与其位置坐标x的关系曲线如图丙所示，其中Ep0和x0皆为已知量，请根据图丙中Ep-x图像提供的信息求解本题中弹簧的劲度系数k′。

（2）若水平面不光滑，小滑块与水平面间的动摩擦因数为μ。如图丁所示，弹簧的劲度系数为k，O为弹簧原长位置，以距O点右侧 的O′为坐标原点，向右为正方向建立坐标轴O′x′。将小滑块沿水平面向右拉到O′右侧的P点，由静止释放小滑块，小滑块可以在水平面上往复运动并最终停下。已知重力加速度为g，并可认为滑动摩擦力与最大静摩擦力大小相等。

①证明小滑块被释放后第一次向左的运动的过程中，其受力特点符合以O′为平衡位置的简谐运动的受力条件。并分析如果小滑块在O点最左方停不住，则O到P点距离应满足什么条件；

② 若小滑块被释放后能第2次经过O点而不能第3次经过O点，试分析说明O′到P点距离又应满足什么条件。

Answer 1

【答案】(1) ①-kx2 ,②图见解析 (2) ①l≥,②≤l≤

【解析】

（1）①弹力与x的关系：

F=-kx

因为F-x图像是过原点的直线，则弹簧弹力所做的功

②如图1所示；

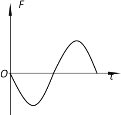
因

则

（2）①

即小滑块第一次向左运动过程的受力情况与以O′为平衡位置的简谐运动的受力相同。

对于小滑块由P点出发向左运动的过程，假设其在最左端时，其距O点的距离为l1，由功能关系得：

即：

解得：

若小滑块速度为零而停不住，则应有：

kl1＞μmg

将l1代入得：

②设小滑块速度为零时距O点的距离为l2，对其由O点左侧最大位移处向右运动至速度减为零的过程，由功能关系得：

解得：

若小滑块到达O点时速度为零，则l2=0，则

滑块能第二次经过O点时满足条件是

同理，小滑块在O点右侧速度为零时距O点的距离为l3，对其由O点右侧最大位移处向左运动至速度减为零的过程，满足

则若小滑块到达O点时速度为零，则32=0，则

滑块不能第三次经过O点时满足条件是

O′到P点距离应满足的条件为

≤l≤。