题目内容
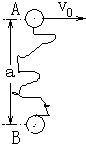 两个质量相同的小球A、B,用长为2a的无弹性且不可伸长的轻绳联结.开始时A、B位于同一竖直线上,B在A的下方,相距为a,如图所示.今给A一个水平速度v0,同时静止释放B.不计空气阻力,且设绳一旦伸直便不再回缩,问经过
两个质量相同的小球A、B,用长为2a的无弹性且不可伸长的轻绳联结.开始时A、B位于同一竖直线上,B在A的下方,相距为a,如图所示.今给A一个水平速度v0,同时静止释放B.不计空气阻力,且设绳一旦伸直便不再回缩,问经过
| ||
| v0 |
| ||
| v0 |
分析:由于A、B两球的加速度大小均为g,且竖直向下.那么以B为参照物观察A的运动是水平向右做匀速直线运动,当绳恰好拉直时,AB球间竖直距离为a,AB间的距离为2a,根据几何关系求出AB球的水平距离,根据t=
即可求解时间.
| x |
| t |
解答:解:由于A、B两球的加速度大小均为g,且竖直向下.那么以B为参照物观察A的运动是水平向右做匀速直线运动,当绳恰好拉直时,AB球间竖直距离为a,
AB间的距离为2a,根据几何关系得:
AB的水平距离为x=
=
a
则经历的时间t=
=
.
故答案为:
.
AB间的距离为2a,根据几何关系得:
AB的水平距离为x=
| (2a)2-a2 |
| 3 |
则经历的时间t=
| x |
| v0 |
| ||
| v0 |
故答案为:
| ||
| v0 |
点评:本题解题的关键是知道A、B两球的加速度大小均为g,且竖直向下.那么以B为参照物观察A的运动是水平向右做匀速直线运动,求出AB球的水平位移即可求解时间,难度不大,属于基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A、球A的线速度必定大于球 B的线速度 | B、球A的角速度必定大于球B的角速度 | C、球A的运动周期必定小于球B的运动周期 | D、球A对筒壁的压力必定大于球B对筒壁的压力 |
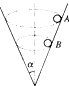 如图所示,在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在各自的水平面内做匀速圆周运动,其中小球A的位置在小球B的上方.下列判断正确的是( )
如图所示,在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在各自的水平面内做匀速圆周运动,其中小球A的位置在小球B的上方.下列判断正确的是( )| A、A球的速率等于B球的速率 | B、A球的角速度大于B球的角速度 | C、A球对漏斗壁的压力等于B球对漏斗壁的压力 | D、A球的转动周期等于B球的转动周期 |
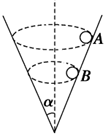 在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,如图所示.下列判断正确的是( )
在光滑的圆锥漏斗的内壁,两个质量相同的小球A和B,分别紧贴着漏斗在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,如图所示.下列判断正确的是( ) 如图所示,两个质量相同的小球A和B,分别用线悬在等高的O1、O2两点,A球的悬线比B球的悬线长,把两球的悬线拉到水平后将小球无初速度释放,则两球经过最低点时( )
如图所示,两个质量相同的小球A和B,分别用线悬在等高的O1、O2两点,A球的悬线比B球的悬线长,把两球的悬线拉到水平后将小球无初速度释放,则两球经过最低点时( )