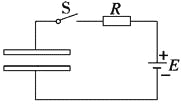
题目内容
【题目】在物资运转过程中常使用传送带.已知某传送带与水平面成θ=37°角,传送带的AB部分长L=29m,传送带以恒定的速率v=10m/s按图示方向传送,若在A端无初速度地放置一个质量m=0.1kg的煤块P(可视为质点),P与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力大小,(g取10m/s2,sin 37°=0.6).求:
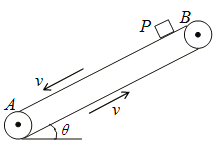
(1)煤块P从B端运动到A端的时间是多少?
(2)若P与传送带之间的动摩擦因数μ=0.8,则煤块P从B端运动到A端的时间又是多少
(3)若P与传送带之间的动摩擦因数μ=0.5,求煤块在传送带上留下的痕迹长度.
【答案】(1)3s(2)3.31s(3)5m
【解析】(1)物体放上传送带后,开始一段时间t1内做初速度为0的匀加速直线运动,小物体受到沿斜面向下的摩擦力:
可知,物体所受合力F合=mgsinθ+f
又因为f=μN=μmgcosθ
所以根据牛顿第二定律可得: ![]()
当物体速度增加到10m/s时产生的位移:x=![]() =5m<29m
=5m<29m
所用时间为:t=v/a=1s
所以物体速度增加到10m/s后,由于mgsinθ>μmgcosθ,所以物体将受沿传送带向上的摩擦力的作用,a2=mgsinθ-μmgcosθ=2m/s2
匀加速运动的位移为29x,设所用时间为t′,
则![]()
解得:t′=2s
t总=1s+2s=3s
(2)若物体与传送带之间的动摩擦因数为0.8,则物体放上传送带后,开始一段时间t′1内做初速度为0的匀加速直线运动,小物体受到沿斜面向下的摩擦力:
可知物体所受合力F′合=mgsinθ+f′
又因为f′=μN=μ′mgcosθ
所以根据牛顿第二定律可得:a′=F′合/m=12.4m/s2
当物体速度增加到10m/s时产生的位移:x′=v22a′=4.03m<29m
所用时间为:t′=v/a′=0.81s
所以物体速度增加到10m/s后,由于mgsinθ<μmgcosθ,所以物体将和传送到一起匀速运动,
匀速运动的位移为29x′,设所用时间为t″,则t″=294.0310=2.50s
则t′总=0.81+2.50=3.31s,
(3)第一阶段炭块的速度小于皮带速度,炭块相对皮带向上移动,炭块的位移为:x=v2/2a=5m
传送带的位移为x′=vt=10×1=10m,故炭块相对传送带上移5m;
第二阶段炭块的速度大于皮带速度,炭块相对皮带向下移动,炭块的位移为:
![]() ,
,
传送带的位移为20m,所以相对于传送带向下运动4m,
故传送带表面留下黑色炭迹的长度为5m;