Question

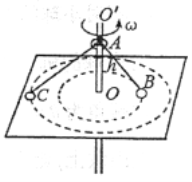
【题目】如图所示，竖直转轴OO'垂直于光滑水平面，A是距O高h的轴上的一点，A点固定有两铰链。两轻质细杆的一端接到铰链上，并可绕铰链上的光滑轴在竖直面内转动，细杆的另一端分别固定质量均为m的小球B 和C，杆长AC>AB>h。当OO'转轴动时，B，C两小球以O为圆心在桌面上做圆周运动，在OO'轴的角速度ω 由零缓慢增大的过程中，下列说法正确的是( )

A. 两小球线速度大小总相等

B. 两小球向心加速度的大小总相等

C. 在ω逐渐增大的过程中，小球C先离开桌面

D. 当ω =时，两小球对桌面均无压力

Answer 1

【答案】D

【解析】

两小球同轴转动，角速度相同，根据v=ωr和a=ω2r比较线速度和向心加速度；当小球恰离开桌面时，根据牛顿第二定律求解临界角速度可判断选项CD.

两球转动的角速度相同，根据v=ωr可知两小球线速度大小不相等，根据a=ω2r可知两小球向心加速度的大小也不相等，选项AB错误；当小球恰好离开桌面时满足：（θ为细杆与竖直方向的夹角）解得，可知在ω逐渐增大的过程中，两小球一起离开桌面，即当ω =时，两小球对桌面均无压力，选项C错误，D正确；故选D.