题目内容
14.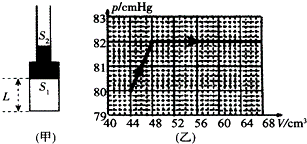 如图甲所示为“⊥”型上端开口的玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中粗细部分截面积分别为S1=2cm2、S2=1cm2.封闭气体初始温度为57℃,气体长度为L=22cm,乙图为对封闭气体缓慢加热过程中气体压强随体积变化的图线.(摄氏温度t与热力学温度T的关系是T=t+273K)求:
如图甲所示为“⊥”型上端开口的玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中粗细部分截面积分别为S1=2cm2、S2=1cm2.封闭气体初始温度为57℃,气体长度为L=22cm,乙图为对封闭气体缓慢加热过程中气体压强随体积变化的图线.(摄氏温度t与热力学温度T的关系是T=t+273K)求:(Ⅰ)封闭气体初始状态的压强;
(Ⅱ)若缓慢升高气体温度,升高至多少方可将所有水银全部压入细管内.
(Ⅲ)当温度升高至492k时,液柱下端离开粗细接口处的距离.
分析 (Ⅰ)根据题意,由图示图象可以求出气体的压强;
(Ⅱ)求出气体的状态参量,然后由理想气体状态方程求出气体的温度;
(Ⅲ)气体发生等压变化,应用盖吕萨克定律求出气体的体积,然后求出高度.
解答 解:(Ⅰ)初始状态封闭的气体,温度:T1=273+57=330K,
体积为:V1=LS1=44cm3,由图示图象可知,此时气体压强:p1=80cmHg…①
(Ⅱ)当水银全部进入细管后,气体将做等压变化,故从图乙可知当所有水银全部进入细管内时,
其封闭的气体压强:p2=82cmHg,体积:V2=48cm3 …②
由理想气体状态方程得:$\frac{{p}_{1}{V}_{1}}{{T}_{1}}$=$\frac{{p}_{2}{V}_{2}}{{T}_{2}}$…③
代入数据解得:T2=369K…④
(Ⅲ)当温度升高至:T3=492K时,水银已经全部在细管内,封闭气体做等压变化,此时气体的体积为V3,由盖吕萨克定律得:$\frac{{V}_{2}}{{T}_{2}}$=$\frac{{V}_{3}}{{T}_{3}}$…⑤
解得:V3=64cm3…⑥
气体体积:V3=V2+S2hx …⑦
代入数据解得:hx=16cm…⑧
答:(Ⅰ)封闭气体初始状态的压强为80cmHg;
(Ⅱ)若缓慢升高气体温度,升高至369K方可将所有水银全部压入细管内.
(Ⅲ)当温度升高至492k时,液柱下端离开粗细接口处的距离为16cm.
点评 本题考查了气体状态方程的应用,找出各个状态下的参量是正确解题的关键,熟练应用理想气体状态方程即可正确解题.

练习册系列答案
相关题目
4.下列每组中三个物理量均为矢量的是( )
| A. | 位移、加速度、电场强度 | B. | 力、动能、磁感应强度 | ||
| C. | 功、动能、势能 | D. | 质量、时间、位移 |
9.下面有关物理学史、物理学思想与方法、物理学概念与理论的说法正确的有( )
| A. | 库仑最早提出与应用电场线来描绘电场 | |
| B. | 电场强度是比值定义的物理量,而电势则不是 | |
| C. | 公式U=Ed由匀强电场导出,所以只适应于匀强电场 | |
| D. | 万有引力常量与静电力常量的测量在装置和原理上是相似的 |
19.下列说法正确的是 ( )
| A. | 放热的物体,其内能也可能增加 | |
| B. | 能量耗散是从能量转化的角度反映出自然界中宏观过程具有的方向性 | |
| C. | 热量不可能从低温物体传递到高温物体 | |
| D. | 已知气体分子间的作用力表现为引力,若气体等温膨胀,则气体对外做功且内能增加 | |
| E. | 温度是分子平均动能的标志,温度升高,则物体的每一个分子的动能都增大. |
 A行星和B行星半径之比为2:3,各有一个卫星绕其运行,运行高度均等于各自行星的半径,已知两个卫星的周期之比为3:2,求行星A和行星B表面处的重力加速度大小之比为多少?
A行星和B行星半径之比为2:3,各有一个卫星绕其运行,运行高度均等于各自行星的半径,已知两个卫星的周期之比为3:2,求行星A和行星B表面处的重力加速度大小之比为多少?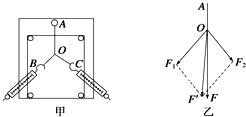 在《探究共点力合成的规律》的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB与OC为细绳,
在《探究共点力合成的规律》的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB与OC为细绳,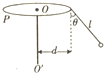 游乐场中有一种叫“空中飞椅”的设施,其基本装置是将绳子上端固定在转盘的边缘上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看成质点,简化为如图所示的模型,其中P为处于水平面内的转盘,可绕竖直转轴OO′转动,已知绳长为l,质点的质量为m,转盘静止时悬绳与转轴间的距离为d.在人与转盘一起做匀速圆周运动时,绳与竖直方向的夹角为θ,不计空气阻力及绳重,绳子不可伸长,则此时绳子的拉力是$\frac{mg}{cosθ}$,圆盘的角速度是$\sqrt{\frac{gtanθ}{d+lsinθ}}$.
游乐场中有一种叫“空中飞椅”的设施,其基本装置是将绳子上端固定在转盘的边缘上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看成质点,简化为如图所示的模型,其中P为处于水平面内的转盘,可绕竖直转轴OO′转动,已知绳长为l,质点的质量为m,转盘静止时悬绳与转轴间的距离为d.在人与转盘一起做匀速圆周运动时,绳与竖直方向的夹角为θ,不计空气阻力及绳重,绳子不可伸长,则此时绳子的拉力是$\frac{mg}{cosθ}$,圆盘的角速度是$\sqrt{\frac{gtanθ}{d+lsinθ}}$.