题目内容
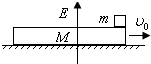 如图所示的水平地面上存在着一方向竖直向上的匀强电场,其场强E=5×106V/m,有一质量为M=8kg的木板,其长为L=1.5m,高为h=0.3m,上表面光滑,木板与地面间的动摩擦因数为μ=0.4.最初木板在水平地面上向右运动,当木板运动的速度大小为v0=4m/s时,把一质量m=3kg的光滑小铁块(可视为质点)轻轻地放在木板上表面的右端,小铁块带有q=+2×10-6 C的电量,设整个过程小铁块的电量不变(g=10m/s2).求
如图所示的水平地面上存在着一方向竖直向上的匀强电场,其场强E=5×106V/m,有一质量为M=8kg的木板,其长为L=1.5m,高为h=0.3m,上表面光滑,木板与地面间的动摩擦因数为μ=0.4.最初木板在水平地面上向右运动,当木板运动的速度大小为v0=4m/s时,把一质量m=3kg的光滑小铁块(可视为质点)轻轻地放在木板上表面的右端,小铁块带有q=+2×10-6 C的电量,设整个过程小铁块的电量不变(g=10m/s2).求(1)小铁块刚放上时木板的加速度大小;
(2)小铁块与木板刚脱离时木板的速度大小;
(3)小铁块刚着地时与木板左端的距离.
分析:对M受力分析,利用牛顿第二定律求解出M的加速度;小铁块与木板刚脱离前木板将做匀减速运动,由运动学公式求解出木板的速度;当小铁块脱离木板时,判断出小铁块下落到地面的时间与木板停止运动所需时间的关系,然后再利用运动学公式求解
解答:解:(1)对M受力分析,有:
FN=Mg+mg-qE=8×10+3×10-2×10-6×5×106=100N
M受到的摩擦力为:
f=μFN=0.4×100N=40N
由牛顿第二定律可知M产生的加速度为:
f=Ma
a=
=
m/s2=5m/s2
(2)小铁块与木板刚脱离时木板前进的位移为s=1.5m
2as=v2
代入数据得:v=1m/s
(3)小铁块与木板刚脱离后,木块自由下落的时间由h=
gt2得
t=
=
s=0.1
s
木板的加速度为
由-μMg=Ma1得
a1=-μg=-4m/s2
木板减速到零所需时间为
t′=
=
s=
s>t
铁块刚着地时与木板左端的距离为
x=vt+
a1t2=0.125m
答:(1)小铁块刚放上时木板的加速度为5m/s2;
(2)小铁块与木板刚脱离时木板的速度1m/s
(3)小铁块刚着地时与木板左端的距离0.125m.
FN=Mg+mg-qE=8×10+3×10-2×10-6×5×106=100N
M受到的摩擦力为:
f=μFN=0.4×100N=40N
由牛顿第二定律可知M产生的加速度为:
f=Ma
a=
| f |
| M |
| 40 |
| 8 |
(2)小铁块与木板刚脱离时木板前进的位移为s=1.5m
2as=v2
| -v | 2 0 |
代入数据得:v=1m/s
(3)小铁块与木板刚脱离后,木块自由下落的时间由h=
| 1 |
| 2 |
t=
|
|
| 6 |
木板的加速度为
由-μMg=Ma1得
a1=-μg=-4m/s2
木板减速到零所需时间为
t′=
| 0-v |
| a1 |
| 0-1 |
| -4 |
| 1 |
| 4 |
铁块刚着地时与木板左端的距离为
x=vt+
| 1 |
| 2 |
答:(1)小铁块刚放上时木板的加速度为5m/s2;
(2)小铁块与木板刚脱离时木板的速度1m/s
(3)小铁块刚着地时与木板左端的距离0.125m.
点评:解决该题关键要对物体进行受力分析,运用运动学公式求解,注重时间条件的判断是关键.

练习册系列答案
相关题目
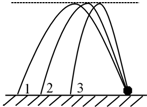 如图所示,水平地面上不同位置的三个小球斜上抛,沿三条不同的路径运动最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个小球斜上抛,沿三条不同的路径运动最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )| A、三个小球落地时的速率相等 | B、沿路径3抛出的小球在空中运动时间最长 | C、三个小球抛出的初速度竖直分量相等 | D、三个小球抛出的初速度水平分量相等 |
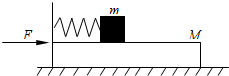 如图所示,水平地面上放置一左边固定有竖直挡板的长木板,在长木板上放一小块木块,它们之间用一轻弹簧相连,现用大小为F的水平恒力向右推长木板,当它们达到相对静止且保持相同的加速度一起加速运动时撤去水平力F.已知长木板的质量为M,小木板的质量为m,所有接触面不计摩擦,则刚撤去水平力F瞬间关于两物体的加速度大小和方向下列说法中正确的是( )
如图所示,水平地面上放置一左边固定有竖直挡板的长木板,在长木板上放一小块木块,它们之间用一轻弹簧相连,现用大小为F的水平恒力向右推长木板,当它们达到相对静止且保持相同的加速度一起加速运动时撤去水平力F.已知长木板的质量为M,小木板的质量为m,所有接触面不计摩擦,则刚撤去水平力F瞬间关于两物体的加速度大小和方向下列说法中正确的是( )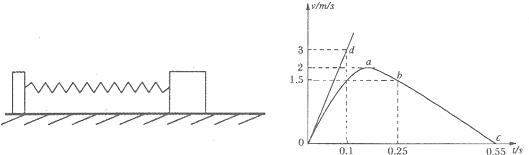
 (2008?滨州二模)如图所示,水平地面上固定着一竖直立柱,某人通过柱顶的定滑轮将200N的重物拉住不动,已知人拉着绳的一端,绳与水平地面夹角为30°,则定滑轮所受的压力大小为( )
(2008?滨州二模)如图所示,水平地面上固定着一竖直立柱,某人通过柱顶的定滑轮将200N的重物拉住不动,已知人拉着绳的一端,绳与水平地面夹角为30°,则定滑轮所受的压力大小为( )