Question

（10分）现有甲、乙两个小球（可视为质点），它们之间存在大小恒定的引力F。已知甲球质量为3m，乙球质量为m。A、B为光滑水平面上的两点，距离为L。某时刻甲球以向左的速度v₀经过A点，同时乙球以向右的速度v₀经过B点，求：

（1）甲球加速度的大小；

（2）当两球相距最远时，甲球速度的大小；

（3）甲、乙两球的最大距离。

 

Answer 1

【答案】

        

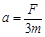
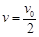
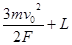
【解析】

试题分析：（1）对甲受力分析知：在竖直方向受到平衡力的作用，在水平方向受到一个引力作用：根据牛顿第二定律可知，甲球的加速度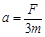

（2）当两球间距离达到最大时，两球的速度相同，设此速度为v。取甲、乙两球为系统，系统合外力为零，所以系统动量守恒。取水平向左为正方向，则有：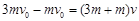   

所以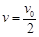

（3）设经过时间t，两球间距离达到最大，则有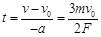

在这段时间中，甲球向左运动的距离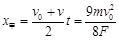

乙球向右运动的距离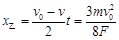

所以两球的最大距离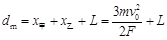

考点：本题考查牛顿第二定律、动量守恒、匀变速直线运动规律。