题目内容
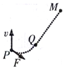
11. 如图,用细线吊着小球,使小球在水平面内做匀速圆周运动(也称为圆锥摆运动),已知小球质量为m,且可视为质点,绳长为L,绳子与竖直方向夹角为θ,重力加速度为g,求:
如图,用细线吊着小球,使小球在水平面内做匀速圆周运动(也称为圆锥摆运动),已知小球质量为m,且可视为质点,绳长为L,绳子与竖直方向夹角为θ,重力加速度为g,求:(1)绳的拉力大小F;
(2)小球圆周运动的周期T.
分析 小球受重力和拉力两个力作用,靠两个力的合力提供向心力,根据平行四边形定则求出绳子的拉力大小,根据牛顿第二定律求出小球做圆周运动的周期.
解答 解:(1)小球的受力如图所示,根据平行四边形定则知,$\frac{mg}{F}=cosθ$,
解得F=$\frac{mg}{cosθ}$.
(2)小球在水平面内做匀速圆周运动,有:
$mgtanθ=mr\frac{4{π}^{2}}{{T}^{2}}$,
r=Lsinθ,
联立解得T=$2π\sqrt{\frac{Lcosθ}{g}}$.
答:(1)绳的拉力大小F为$\frac{mg}{cosθ}$;
(2)小球圆周运动的周期T为$2π\sqrt{\frac{Lcosθ}{g}}$.
点评 解决本题的关键知道小球做匀速圆周运动向心力的来源,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
相关题目
1.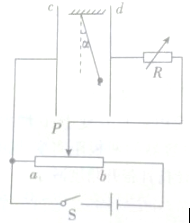 如图所示,两块平行金属板c,d竖直放置,其间有用绝缘细线悬挂的带电小球,闭合开关,滑片P位于ab正中间时,小球偏离竖直方向α角,则( )
如图所示,两块平行金属板c,d竖直放置,其间有用绝缘细线悬挂的带电小球,闭合开关,滑片P位于ab正中间时,小球偏离竖直方向α角,则( )
 如图所示,两块平行金属板c,d竖直放置,其间有用绝缘细线悬挂的带电小球,闭合开关,滑片P位于ab正中间时,小球偏离竖直方向α角,则( )
如图所示,两块平行金属板c,d竖直放置,其间有用绝缘细线悬挂的带电小球,闭合开关,滑片P位于ab正中间时,小球偏离竖直方向α角,则( )| A. | 保持滑片P位置不变,在紧靠板c处插入电介质,α角将变小 | |
| B. | 仅断开开关,α角将不变 | |
| C. | 仅调节电阻箱R使其阻值增大,α角将变大 | |
| D. | 仅将滑片向b端移动时,α角将变大 |
2.下列表述不符合物理史实的是( )
| A. | 伽利略提出了太阳系行星运动的第三大定律 | |
| B. | 牛顿提出了万有引力定律 | |
| C. | 卡文迪许首先测出了万有引力常量 | |
| D. | 爱因斯坦建立狭义相对论 |
19.下面列举的情况中所做的功不为零的是( )
| A. | 自由落体运动中,重力对物体做的功 | |
| B. | 汽车沿斜坡向上运动时,斜坡支持力对汽车做的功 | |
| C. | 举重运动员,举着杠铃在头上方停留3s,运动员对杠铃做的功 | |
| D. | 用手指捏住玻璃板竖直向上提起时,手指对玻璃板的压力做的功 |
6.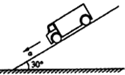 一汽车沿着倾角为30°的斜面向下匀加速直线运动,若测得该车得加速度a=6m/s2,重力加速度g=10m/s2,那么,由此判断该汽车机械能的变化情况是( )
一汽车沿着倾角为30°的斜面向下匀加速直线运动,若测得该车得加速度a=6m/s2,重力加速度g=10m/s2,那么,由此判断该汽车机械能的变化情况是( )
 一汽车沿着倾角为30°的斜面向下匀加速直线运动,若测得该车得加速度a=6m/s2,重力加速度g=10m/s2,那么,由此判断该汽车机械能的变化情况是( )
一汽车沿着倾角为30°的斜面向下匀加速直线运动,若测得该车得加速度a=6m/s2,重力加速度g=10m/s2,那么,由此判断该汽车机械能的变化情况是( )| A. | 机械能守恒 | B. | 机械能减小 | C. | 机械能增加 | D. | 无法判断 |
3.关于生活中的圆周运动,下列说法正确的是( )
| A. | 转速很高的切割砂轮半径越大越好 | |
| B. | 在水平公路上转弯时汽车速度过大将做离心运动而造成事故 | |
| C. | 在修筑铁路时,转弯处铁轨的内轨要低于外轨是为了减轻火车轮缘与外轨的挤压 | |
| D. | 市内公共汽车转弯前提醒“车辆转弯,请拉好扶手”是防止站立的乘客转弯时向内侧倾倒 |
20.物体以速度v0水平抛出,若不计空气阻力,则当其竖直方向的位移与水平方向的位移相等时,以下说法中不正确的是( )
| A. | 竖直分速度为$\sqrt{2}$v0 | B. | 即时速度大小为$\sqrt{5}$v0 | ||
| C. | 运动的时间为$\frac{2{v}_{0}}{g}$ | D. | 运动的位移为$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ |
5.(多选题)下列关于振动和波的说法中正确的是( )
| A. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关 | |
| B. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| C. | 当一列声波从空气中传入水中时波长一定会变短 | |
| D. | 麦克斯韦预言了电磁波的存在,赫兹通过实验证实 |