题目内容
质量为 1.0×103kg 的汽车,沿倾角为 30°的斜坡由静止开始向上运动,汽车在运动过程中所受阻力大小恒为 2.0×103N,汽车发动机的额定输出功率为 5.6×104W,开始时以 a=1.0m/s2的加速度做匀加速运动(g=10m/s2).求:
(1)汽车所能达到的最大速率;
(2)汽车做匀加速运动的时间t1.
(1)汽车所能达到的最大速率;
(2)汽车做匀加速运动的时间t1.
分析:(1)当汽车所受的合力为零时,汽车的速度最大,根据平衡求出牵引力的大小,从而根据P=Fv求出最大速率.
(2)根据牛顿第二定律求出牵引力的大小,结合P=Fv求出匀加速直线运动的最大速度,从而根据速度时间公式求出匀加速直线运动的时间.
(2)根据牛顿第二定律求出牵引力的大小,结合P=Fv求出匀加速直线运动的最大速度,从而根据速度时间公式求出匀加速直线运动的时间.
解答:解:(1)当汽车的加速度为零时,有:F=mgsin30°+f=1×104×
+2×103N=7×103N.
则汽车达到的最大速率vm=
=
m/s=8m/s.
(2)根据牛顿第二定律得,F-mgsin30°-f=ma得,
F=mgsin30°+f+ma=1×104×
+2×103+1×103N=8×103N.
在匀加速直线运动的最大速度vm1=
=
m/s=7m/s.
则匀加速直线运动的时间t1=
=
s=7s.
答:(1)汽车能达到的最大速率为8m/s.(2)汽车做匀加速直线运动的时间为7s.
| 1 |
| 2 |
则汽车达到的最大速率vm=
| P |
| F |
| 5.6×104 |
| 7×103 |
(2)根据牛顿第二定律得,F-mgsin30°-f=ma得,
F=mgsin30°+f+ma=1×104×
| 1 |
| 2 |
在匀加速直线运动的最大速度vm1=
| P |
| F |
| 5.6×104 |
| 8×103 |
则匀加速直线运动的时间t1=
| vm1 |
| a |
| 7 |
| 1 |
答:(1)汽车能达到的最大速率为8m/s.(2)汽车做匀加速直线运动的时间为7s.
点评:解决本题的关键知道加速度为零时,速度最大,结合P=Fv求解,注意F为牵引力的大小.

练习册系列答案
相关题目
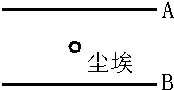 水平放置的平行板电容器,两极板A、B相距5mm,电容为2μF,求:
水平放置的平行板电容器,两极板A、B相距5mm,电容为2μF,求: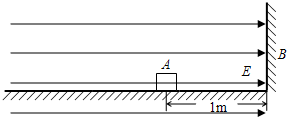 如图所示,物块A(可视为质点)的质量为1.0×10-2kg,带1.0×10-8C的正电荷.A与水平桌面间的动摩擦因数为μ=0.2,B为竖直挡板,A与挡板相距1.0m.A以6m/s的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=8.0×106N/C.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始到最后停止的过程中
如图所示,物块A(可视为质点)的质量为1.0×10-2kg,带1.0×10-8C的正电荷.A与水平桌面间的动摩擦因数为μ=0.2,B为竖直挡板,A与挡板相距1.0m.A以6m/s的速度向B运动,在A运动的空间里存在着水平向右的匀强电场,场强E=8.0×106N/C.设A与B相碰无机械能损失,A在运动中电量不变.求物块A从图示位置开始到最后停止的过程中 用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2kg,所带电荷量为+2.0×10-8C.现加一水平方向的匀速电场,平衡时绝缘绳与铅垂线成45°求这个匀强电场的电场强度.
用一条绝缘轻绳悬挂一个带电小球,小球质量为1.0×10-2kg,所带电荷量为+2.0×10-8C.现加一水平方向的匀速电场,平衡时绝缘绳与铅垂线成45°求这个匀强电场的电场强度.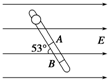 如图所示,一个质量为1.0×10-4kg的带电小球,穿过一根光滑的绝缘杆,置于场强为2.0×102N/C的水平向右的匀强电场中,杆与水平面夹角为53°,小球刚好匀速下滑,问:(sin 53°=0.8,cos 53°=0.6)
如图所示,一个质量为1.0×10-4kg的带电小球,穿过一根光滑的绝缘杆,置于场强为2.0×102N/C的水平向右的匀强电场中,杆与水平面夹角为53°,小球刚好匀速下滑,问:(sin 53°=0.8,cos 53°=0.6)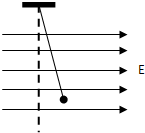 用一根绝缘轻绳悬挂一个带电小球,小球的质量为1.0×10-2㎏,所带的电荷量为+3.0×10-8C.现加一水平方向的匀强电场,小球平衡时绝缘绳与竖直线成37°,如图所示,求该匀强电场的电场强度的大小并作受力分析图.(g=10m/s2,sin37°=0.6,cos37°=0.8)
用一根绝缘轻绳悬挂一个带电小球,小球的质量为1.0×10-2㎏,所带的电荷量为+3.0×10-8C.现加一水平方向的匀强电场,小球平衡时绝缘绳与竖直线成37°,如图所示,求该匀强电场的电场强度的大小并作受力分析图.(g=10m/s2,sin37°=0.6,cos37°=0.8)