题目内容
20.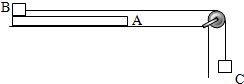 如图所示,在光滑的水平桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3kg的金属块B,A的长度L=2.0m,B上有轻线绕过定滑轮与质量为mC=1.0kg的物块C相连,B与A之间的动摩擦因数μ=0.10,最大静摩擦力可视为等于滑动摩擦力,忽略滑轮质量及与轴间的摩擦,起始时各物体都处于静止状态,绳被拉直,B位于A的左端(如图),然后释放.(g=10m/s2)
如图所示,在光滑的水平桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3kg的金属块B,A的长度L=2.0m,B上有轻线绕过定滑轮与质量为mC=1.0kg的物块C相连,B与A之间的动摩擦因数μ=0.10,最大静摩擦力可视为等于滑动摩擦力,忽略滑轮质量及与轴间的摩擦,起始时各物体都处于静止状态,绳被拉直,B位于A的左端(如图),然后释放.(g=10m/s2)(1)若将薄木板A固定在水平桌面上,求B在A板上运动的时间t1;
(2)若薄木板A未固定在桌面上,求B在A板上运动的时间t2(设A的右端距滑轮足够远).
分析 (1)利用牛顿第二定律求得BC的共同加速度,利用位移时间公式求得运动时间;
(2)利用牛顿第二定律求得A的加速度,利用位移时间公式求得脱离时间;
解答 解:(1)A固定,BC整体的加速度为:
${a}_{1}=\frac{{m}_{C}g-μ{m}_{B}g}{{m}_{B}+{m}_{C}}=1.75m/{s}^{2}$
从释放到脱离,有:L=$\frac{1}{2}{{a}_{1}t}_{1}^{2}$
解得:${t}_{1}=\frac{4\sqrt{7}}{7}s$
(2)AB发生相对滑动,A的加速度为:
${a}_{2}=\frac{μ{m}_{B}g}{{m}_{A}}=1.5m/{s}^{2}$
从释放到B从A的右端脱离,则有:
$L=\frac{1}{2}{{a}_{1}t}_{2}^{2}-\frac{1}{2}{{a}_{2}t}_{2}^{2}$
代入数据解得:t2=4s
答:(1)若将薄木板A固定在水平桌面上,求B在A板上运动的时间t1为$\frac{4\sqrt{7}}{7}$s
(2)若薄木板A未固定在桌面上,求B在A板上运动的时间t2为4s
点评 本题考查了牛顿第二定律和运动学公式的综合运用,关键在于合理地选择研究对象,通过牛顿第二定律求出加速度.

练习册系列答案
相关题目
18.一个质点做直线运动,其位移随时间变化的规律为x=4t-t2(m),其中时间t的单位为s,则当质点的速度为2m/s时,质点运动的位移为( )
| A. | -2m | B. | 2m | C. | -3m | D. | 3m |
19.用同种材料制成倾角为30°的斜面和长水平面,斜面长2.4m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过0.8s后小物块停在斜面上.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t-v0图象,如图所示,则下列说法中正确的是(g=10m/s2)( )
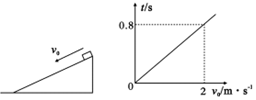

| A. | 小物块在斜面上运动时加速度大小为2.5m/s2 | |
| B. | 小物块在斜面上运动时加速度大小为0.4m/s2 | |
| C. | 小物块与该种材料间的动摩擦因数为0.5 | |
| D. | 由图可推断若小物块初速度继续增大,小物块的运动时间也随速度均匀增大 |
8.根据如表提供的信息回答.(提示:表格中第3行“20”“30”表示速度,它们下面的数据表示制动距离)(结果保留一位小数)
(1)从表中查出质量为4.5t的汽车,以20km/h的速度空载行驶时的制动距离,求地面对汽车的阻力不得小于多少?
(2)从表中查出一辆总质量4.0t的轿车,以30km/h的速度满载行驶时的制动距离,若该轿车以60km/h速度行驶,求其满载时制动距离允许最大值是多大?
| 机动车的类型 | 各检验项目和速度限值v/(km•h-1) | |||
| 空载检验的制动距离x/m | 满载检验的制动距离x/m | |||
| 20km•h-1 | 30km•h-1 | 20km•h-1 | 30km•h-1 | |
| 总质量<4.5t | ≤6.5 | ≤7.0 | ||
| 4.5t≤总质量≤12t的汽车和无轨电车 | ≤3.8 | ≤8.0 | ||
| 总质量>12t的汽车和无轨电车 | ≤4.4 | ≤9.5 | ||
(2)从表中查出一辆总质量4.0t的轿车,以30km/h的速度满载行驶时的制动距离,若该轿车以60km/h速度行驶,求其满载时制动距离允许最大值是多大?
15.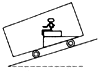 为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )
为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )
 为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )
为了让乘车更为舒适,某探究小组设计了一种新的交通工具,如图所示,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,当此车加速下坡时,盘腿坐在座椅上的一位乘客( )| A. | 乘客所受合外力可能竖直向下 | B. | 支持力可能大于重力 | ||
| C. | 受到向前(水平向左)的摩擦力作用 | D. | 可能处于超重状态 |
5.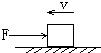 如图所示,质量m=20kg的物体在水平地面上向左运动.物体与水平面间的动摩擦因数为0.1,与此同时物体受到一个水平向右的F=40N的推力作用,则物体的加速度是(g取10m/s2)( )
如图所示,质量m=20kg的物体在水平地面上向左运动.物体与水平面间的动摩擦因数为0.1,与此同时物体受到一个水平向右的F=40N的推力作用,则物体的加速度是(g取10m/s2)( )
 如图所示,质量m=20kg的物体在水平地面上向左运动.物体与水平面间的动摩擦因数为0.1,与此同时物体受到一个水平向右的F=40N的推力作用,则物体的加速度是(g取10m/s2)( )
如图所示,质量m=20kg的物体在水平地面上向左运动.物体与水平面间的动摩擦因数为0.1,与此同时物体受到一个水平向右的F=40N的推力作用,则物体的加速度是(g取10m/s2)( )| A. | 0 | B. | 4m/s2,水平向右 | C. | 3m/s2,水平向左 | D. | 3m/s2,水平向右 |
12.有两个惯性参考系1和2,彼此相对做匀速直线运动,下列叙述正确的是( )
| A. | 在参考系1看来,2中的所有物理过程都变快了;在参考系2看来,1中的所有物理过程都变慢了 | |
| B. | 在参考系1看来,2中的所有物理过程都变快了;在参考系2看来,1中的所有物理过程也变快了 | |
| C. | 在参考系1看来,2中的所有物理过程都变慢了;在参考系2看来,1中的所有物理过程都变快了 | |
| D. | 在参考系1看来,2中的所有物理过程都变慢了;在参考系2看来,1中的所有物理过程也变慢了 |
9.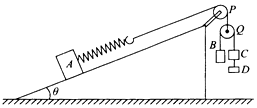 如图所示,在倾角为θ的粗糙斜面上放置与轻弹簧相连的物体A,弹簧另一端通过轻绳连接到轻质定滑轮Q上,三个物体B、C、D通过绕过定滑轮Q的轻绳相连而处于静止状态.现将物体D从C的下端取下挂在B上,松手后物体A扔处于静止状态,若不计轮轴与滑轮.绳与滑轮间的摩擦,则下列有关描述正确的是( )
如图所示,在倾角为θ的粗糙斜面上放置与轻弹簧相连的物体A,弹簧另一端通过轻绳连接到轻质定滑轮Q上,三个物体B、C、D通过绕过定滑轮Q的轻绳相连而处于静止状态.现将物体D从C的下端取下挂在B上,松手后物体A扔处于静止状态,若不计轮轴与滑轮.绳与滑轮间的摩擦,则下列有关描述正确的是( )
 如图所示,在倾角为θ的粗糙斜面上放置与轻弹簧相连的物体A,弹簧另一端通过轻绳连接到轻质定滑轮Q上,三个物体B、C、D通过绕过定滑轮Q的轻绳相连而处于静止状态.现将物体D从C的下端取下挂在B上,松手后物体A扔处于静止状态,若不计轮轴与滑轮.绳与滑轮间的摩擦,则下列有关描述正确的是( )
如图所示,在倾角为θ的粗糙斜面上放置与轻弹簧相连的物体A,弹簧另一端通过轻绳连接到轻质定滑轮Q上,三个物体B、C、D通过绕过定滑轮Q的轻绳相连而处于静止状态.现将物体D从C的下端取下挂在B上,松手后物体A扔处于静止状态,若不计轮轴与滑轮.绳与滑轮间的摩擦,则下列有关描述正确的是( )| A. | 物体D挂在物体B下面比D挂在C下面时,物体A所受的摩擦力减小了 | |
| B. | 物体D挂在物体B下面比D挂在C下面时,弹簧的形变量减小了 | |
| C. | 物体D挂在物体B下面比D挂在C下面时,地面对斜面体的支持力减小了 | |
| D. | 物体D挂在物体B下面比D挂在C下面时,地面对斜面体有向左的摩擦力 |
10.下列说法正确的是( )
| A. | 洛伦兹发明了回旋加速器 | |
| B. | 光电效应现象说明光具有粒子性 | |
| C. | 密立根通过油滴实验测出了电子的质量 | |
| D. | 卢瑟福通过α粒子散射实验得出了原子核是由质子和中子组成的 |