题目内容
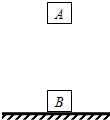
 有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)
有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)
(1)当A静止于B的正上方时,两者间的距离x1多大;
(2)当A静止于B的正上方时,给A施加一个竖直向上的拉力,使A向上做匀加直线运动,加速度大小为a,则经过多长时间,B开始离开地面;
(3)若把A从B的正上方相距x0处由静止释放,则A向下运动的过程中所能达到的最大速度vm为多少.
解:
(1)当A静止于B的正上方时,它一定是在重力和B的斥力作用下平衡,则有:
mg=ρ(x0-x1)
解得: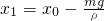
(2)当B离开地面时,B受到A的引力等于B的重力,
即 mg=ρ(x2-x0)
故此时AB间的距离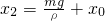
在A匀加速上升过程中: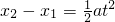
解得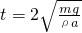
(3)A释放后开始向下做变加速直线运动,当AB相距为x1时速度达到最大,此过程中: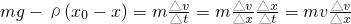
变形为:(mg-ρx0)△x+ρx△x=mv△v
对上式进行积分得: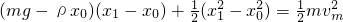
化简得:A所能达到的最大速度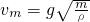
答:
(1)当A静止于B的正上方时,两者间的距离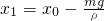 ;
;
(2)当A静止于B的正上方时,给A施加一个竖直向上的拉力,使A向上做匀加直线运动,加速度大小为a,经过时间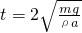 ,B开始离开地面;
,B开始离开地面;
(3)若把A从B的正上方相距x0处由静止释放,A向下运动的过程中所能达到的最大速度为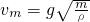 .
.
分析:(1)当A静止于B的正上方时,其重力与斥力平衡,由平衡条件求解两者间的距离x1.
(2)当B离开地面时,B受到A的引力等于B的重力,由F=ρ(x0-x)求出AB间的距离,由位移公式求出运动时间.
(3)A释放后开始向下做变加速直线运动,根据牛顿第二定律得出A、B间距离与速度变化率的关系式,运用积分的方法求出最大速度vm.
点评:本题首先要认真审题,读懂题意.对于变加速运动,不能匀变速运动的公式求速度,常常采用微分、积分的方法求速度.
(1)当A静止于B的正上方时,它一定是在重力和B的斥力作用下平衡,则有:
mg=ρ(x0-x1)
解得:
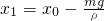
(2)当B离开地面时,B受到A的引力等于B的重力,
即 mg=ρ(x2-x0)
故此时AB间的距离
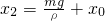
在A匀加速上升过程中:
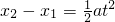
解得
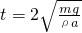
(3)A释放后开始向下做变加速直线运动,当AB相距为x1时速度达到最大,此过程中:
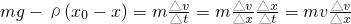
变形为:(mg-ρx0)△x+ρx△x=mv△v
对上式进行积分得:
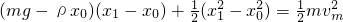
化简得:A所能达到的最大速度
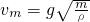
答:
(1)当A静止于B的正上方时,两者间的距离
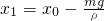 ;
;(2)当A静止于B的正上方时,给A施加一个竖直向上的拉力,使A向上做匀加直线运动,加速度大小为a,经过时间
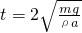 ,B开始离开地面;
,B开始离开地面;(3)若把A从B的正上方相距x0处由静止释放,A向下运动的过程中所能达到的最大速度为
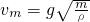 .
.分析:(1)当A静止于B的正上方时,其重力与斥力平衡,由平衡条件求解两者间的距离x1.
(2)当B离开地面时,B受到A的引力等于B的重力,由F=ρ(x0-x)求出AB间的距离,由位移公式求出运动时间.
(3)A释放后开始向下做变加速直线运动,根据牛顿第二定律得出A、B间距离与速度变化率的关系式,运用积分的方法求出最大速度vm.
点评:本题首先要认真审题,读懂题意.对于变加速运动,不能匀变速运动的公式求速度,常常采用微分、积分的方法求速度.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 (2011?江苏模拟)有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)
(2011?江苏模拟)有两个用特殊材料做成的两个物体A和B,质量都为m;它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=ρ(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)