题目内容
【题目】（15分）如图所示，竖直固定的足够长的光滑金属导轨MN、PQ，间距L＝0.2 m，其电阻不计。完全相同的两根金属棒ab、cd垂直导轨放置，每根金属棒两端都与导轨始终良好接触。已知两棒质量均为m＝0.01 kg，电阻均为R＝0.2 Ω，棒cd放置在水平绝缘平台上，整个装置处在垂直于导轨平面向里的匀强磁场中，磁感应强度B＝1.0 T。棒ab在竖直向上的恒力F作用下由静止开始向上运动，当ab棒运动x＝0.1 m时达到最大速度vm，此时cd棒对绝缘平台的压力恰好为零，g取10 m/s2。求：
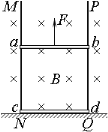
（1）ab棒的最大速度vm；
（2）ab棒由静止到最大速度的过程中通过ab棒的电荷量q；
（3）ab棒由静止到最大速度的过程中回路产生的焦耳热Q。
【答案】（1）vm＝1 m/s（4分） （2）q＝0.05 C（5分） （3）Q＝5×10－3 J（6分）
【解析】（1）当ab棒达到最大速度vm时，对cd棒，受重力和向上的安培力作用，根据共点力平衡条件有：mg＝ILB ①（1分）
对整个回路，根据闭合电路欧姆定律有：E＝2IR ②（1分）
根据法拉第电磁感应定律可知，ab棒切割磁感线产生的感应电动势为：E＝BLvm ③（1分）
由①②③式联立解得：vm＝
＝
m/s＝1 m/s ④（1分）
（2）设ab棒由静止释放后经过时间为t速度达到最大，根据电流强度的定义可知：
＝
⑤（1分）
根据闭合电路欧姆定律可知：
＝
⑥（1分）
根据法拉第电磁感应定律有：
＝
⑦（1分）
由题意可知，在该过程中，穿过回路的磁通量变化量为：ΔΦ＝BLx ⑧（1分）
由⑤⑥⑦⑧式联立解得：q＝
＝
C＝0.05 C （1分）
（3）当ab棒速度达到最大时，其加速度为0，根据牛顿第二定律有：
F－ILB－mg＝0 ⑨（2分）
在ab棒由静止到最大速度的过程中，根据功能关系有：（F－mg）x＝
＋Q ⑩（2分）
由①②③④⑨⑩式联立解得：Q＝
－
＝0.01 J－0.005 J＝5×10－3 J （2分）
综合自测系列答案
