题目内容
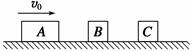
如图所示,光滑水平直轨道上放置长木板B和滑块C,滑块A置于B的左端,且A、B间接触面粗糙,三者质量分别为mA =" 1" kg 、mB =" 2" kg、 mC =" 23" kg .开始时 A、B一起以速度v0 ="10" m/s向右运动,与静止的C发生碰撞,碰后C向右运动,又与竖直固定挡板碰撞,并以碰前速率弹回,此后B与C不再发生碰撞.已知B足够长,A、B、C最终速度相等.求B与C碰后瞬间B的速度大小.
7.25 m/s
解析试题分析:设碰后B速度为vB ,C速度为vC , 以向右为正方向,由动量守恒定律得
mB v0 = mCvC - mB vB
BC碰后,A、B在摩擦力作用下达到共同速度,大小为vC ,由动量守恒定律得
mA v0 - mB vB = -(mA + mB)vC
代入数据得vB =" 7.25" m/s
考点:动量守恒定律。

练习册系列答案
相关题目
质量都为m的小球a、b、c以相同的速度分别与另外三个质量都为M的静止小球相碰后,a球被反向弹回,b球与被碰球粘合在一起仍沿原方向运动,c球碰后静止,则下列说法正确的是( )
| A.m一定大于M |
| B.m可能等于M |
| C.b球与质量为M的球组成的系统损失的动能最大 |
| D.c球与质量为M的球组成的系统损失的动能最大 |
 ,试求:
,试求:
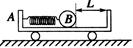
 kg的小车静止在光滑的水平面上,小车上有一质量
kg的小车静止在光滑的水平面上,小车上有一质量 kg的光滑小球,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为
kg的光滑小球,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为 J,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,L=1.2m。求:
J,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,L=1.2m。求: