题目内容
13. 如图所示,在xOy平面内分布着沿y轴正向的匀强电场,虚线是半径r=$\sqrt{2}$a、圆心在(3a,0)的圆.质量为m、电荷量为+q(q>0)的粒子从原点O以速度v0沿x轴正向射出,其运动轨迹恰好与圆相切于点P.不计粒子的重力,求:
如图所示,在xOy平面内分布着沿y轴正向的匀强电场,虚线是半径r=$\sqrt{2}$a、圆心在(3a,0)的圆.质量为m、电荷量为+q(q>0)的粒子从原点O以速度v0沿x轴正向射出,其运动轨迹恰好与圆相切于点P.不计粒子的重力,求:(1)粒子在P点的速度方向与x轴正向的夹角;
(2)匀强电场的场强E的大小.
分析 (1)粒子在电场中做类平抛运动,应用类平抛运动规律求出其轨迹方程,然后根据题意求出与圆的交点,再求出速度方向与x轴正方向的夹角.
(2)应用类平抛运动规律求出电场强度.
解答 解:如下图:过B点作x轴垂线与圆交于P点,过P点做圆G 的切线交x轴于A点;由长度关系可证三角形BPG为等腰直角三角形,所以可得OA=AB=BP;由类平抛运动速度的延长线过水平位移的中点,可知P点即为粒子运动轨迹与圆的交点.
(1)粒子做类平抛运动,由题意可知,
粒子运动轨迹恰好与圆相切于点P,粒子运动轨迹如图所示:
则,粒子的水平位移:x=2a,
由勾股定理得:y2+(3a-2a)2=($\sqrt{2}$a)2,解得:y=a,
粒子在P点的速度方向与x轴正向的夹角的正切值:tanθ=$\frac{y}{\frac{x}{2}}$=$\frac{a}{\frac{2a}{2}}$=1,θ=45°;
(2)粒子做类平抛运动,
水平方向:x=2a=v0t,
竖直方向:y=a=$\frac{1}{2}$$\frac{qE}{m}$t2,
解得:E=$\frac{m{v}_{0}^{2}}{2qa}$;
答:(1)粒子在P点的速度方向与x轴正向的夹角为45;
(2)匀强电场的场强E的大小为$\frac{m{v}_{0}^{2}}{2qa}$.
点评 本题难度较大,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键,应用类平抛运动规律与几何知识可以解题;作出粒子的运动轨迹,轨迹与圆相切与P点,连切点P和圆心,圆心与P的连线是圆的半径,与切线垂直,平抛运动切线的延长线过水平位移的中点,圆的切线与圆半径垂直,这是圆与运动轨迹的共同的切线.

练习册系列答案
相关题目
8.下列说法中正确的是( )
| A. | 参考系就是相对地面静止不动的物体 | |
| B. | 研究跳水运动员在空中姿态时,可以把运动员看作质点 | |
| C. | 物体运动时,平均速度的方向与位移的方向相同 | |
| D. | 亚里士多德早已对自由落体运动作出了科学正确的结论 |
9.下列说法正确的是( )
| A. | 第4s是指3s末到5s初这段时间 | |
| B. | 形状规则的物体的重心必在其几何中心 | |
| C. | 研究牙买加运动员博尔特百米跑步动作时,可把博尔特看成质点 | |
| D. | 我市出租车的收费标准是1.20元/公里,其中“每公里”指的是位移 |
1.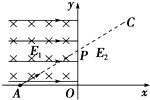 如图,在一竖直平面内,y轴左侧有一水平向右的匀强电场E1和一垂直纸面向里的匀强磁场B,y轴右侧有一竖直方向的匀强电场E2,一电荷量为q(电性未知)、质量为m的微粒从x轴上A点以一定初速度与水平方向成θ=37°角沿直线经P点运动到图中C点,其中m、q、B均已知,重力加速度为g,则( )
如图,在一竖直平面内,y轴左侧有一水平向右的匀强电场E1和一垂直纸面向里的匀强磁场B,y轴右侧有一竖直方向的匀强电场E2,一电荷量为q(电性未知)、质量为m的微粒从x轴上A点以一定初速度与水平方向成θ=37°角沿直线经P点运动到图中C点,其中m、q、B均已知,重力加速度为g,则( )
 如图,在一竖直平面内,y轴左侧有一水平向右的匀强电场E1和一垂直纸面向里的匀强磁场B,y轴右侧有一竖直方向的匀强电场E2,一电荷量为q(电性未知)、质量为m的微粒从x轴上A点以一定初速度与水平方向成θ=37°角沿直线经P点运动到图中C点,其中m、q、B均已知,重力加速度为g,则( )
如图,在一竖直平面内,y轴左侧有一水平向右的匀强电场E1和一垂直纸面向里的匀强磁场B,y轴右侧有一竖直方向的匀强电场E2,一电荷量为q(电性未知)、质量为m的微粒从x轴上A点以一定初速度与水平方向成θ=37°角沿直线经P点运动到图中C点,其中m、q、B均已知,重力加速度为g,则( )| A. | 微粒一定带负电 | B. | 电场强度E2一定竖直向上 | ||
| C. | 两电场强度之比$\frac{{E}_{1}}{{E}_{2}}$=$\frac{4}{3}$ | D. | 微粒的初速度为v=$\frac{5mg}{4Bq}$ |
2. 如图为一位于墙角的固定光滑斜面,其倾角θ=45°,劲度系数为k的轻质弹簧一端系在质量为m的小球上,另一端固定在墙上,弹簧水平放置,小球恰好静止在斜面上,则( )
如图为一位于墙角的固定光滑斜面,其倾角θ=45°,劲度系数为k的轻质弹簧一端系在质量为m的小球上,另一端固定在墙上,弹簧水平放置,小球恰好静止在斜面上,则( )
 如图为一位于墙角的固定光滑斜面,其倾角θ=45°,劲度系数为k的轻质弹簧一端系在质量为m的小球上,另一端固定在墙上,弹簧水平放置,小球恰好静止在斜面上,则( )
如图为一位于墙角的固定光滑斜面,其倾角θ=45°,劲度系数为k的轻质弹簧一端系在质量为m的小球上,另一端固定在墙上,弹簧水平放置,小球恰好静止在斜面上,则( )| A. | 弹簧对小球可能为拉力 | B. | 小球一定受到三个力作用 | ||
| C. | 小球可能受到四个力作用 | D. | 弹簧的形变量为$\frac{mg}{k}$ |
3.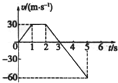 日本“艾普西龙”号固体燃料火箭成功发射了一颗卫星.此前多次发射均告失败,若某次竖直向上发射时火箭发生故障,造成火箭的v-t图象如图所示,则下述说法正确的是( )
日本“艾普西龙”号固体燃料火箭成功发射了一颗卫星.此前多次发射均告失败,若某次竖直向上发射时火箭发生故障,造成火箭的v-t图象如图所示,则下述说法正确的是( )
 日本“艾普西龙”号固体燃料火箭成功发射了一颗卫星.此前多次发射均告失败,若某次竖直向上发射时火箭发生故障,造成火箭的v-t图象如图所示,则下述说法正确的是( )
日本“艾普西龙”号固体燃料火箭成功发射了一颗卫星.此前多次发射均告失败,若某次竖直向上发射时火箭发生故障,造成火箭的v-t图象如图所示,则下述说法正确的是( )| A. | 0~1s内火箭匀加速上升 | B. | 1s~2s内火箭静止不动 | ||
| C. | 3s末火箭回到出发点 | D. | 5s末火箭恰好回到出发点 |


 如图所示,一束电子(电子电量为e)以速度v0垂直射入磁感应强度为B,宽度为d的匀强磁场中,穿过磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是$\frac{2bed}{{V}_{0}}$,穿过磁场的时间是$\frac{πd}{3{V}_{0}}$.如果将磁场变成电场强度为E、方向如图的匀强电场,则电子穿过电场的时间是$\frac{d}{{V}_{0}}$.
如图所示,一束电子(电子电量为e)以速度v0垂直射入磁感应强度为B,宽度为d的匀强磁场中,穿过磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是$\frac{2bed}{{V}_{0}}$,穿过磁场的时间是$\frac{πd}{3{V}_{0}}$.如果将磁场变成电场强度为E、方向如图的匀强电场,则电子穿过电场的时间是$\frac{d}{{V}_{0}}$.