��Ŀ����
10�� ij����90m����60m������ǰ�������ߴ��������ر�����ǰ�߳���������˶�����Ϊ�ڵ����������ٶ�Ϊ12m/s���ȼ���ֱ���˶������ٶȴ�СΪ2m/s2��
ij����90m����60m������ǰ�������ߴ��������ر�����ǰ�߳���������˶�����Ϊ�ڵ����������ٶ�Ϊ12m/s���ȼ���ֱ���˶������ٶȴ�СΪ2m/s2����1��������ӿ�ʼ���ȼ����˶���ͣ������λ��Ϊ���
��2������ʼ���ȼ���ֱ���˶���ͬʱ����ǰ���Ա�ر�����ǰ������ǰ���Ա���������̿���Ϊ���ٶ�Ϊ0�����ٶ�Ϊ2m/s2���ȼ���ֱ���˶������ܴﵽ������ٶ�Ϊ8m/s���ﵽ����ٶȺ���������ٶ������˶������жϸ�ǰ���Ա������ֹͣ�˶�ʱ���Ƿ�������ǰ���Ա���پ����ʱ����������
���� ��1�������ٶ�ʱ�乫ʽ��������ٶȼ�Ϊ���ʱ�䣬���ƽ���ٶ��������ͣ������λ�ƣ�
��2�������ٶ�ʱ�乫ʽ���ǰ���Ա�ٶȴﵽ���ʱ�����ʱ�䣬����ȼ���ֱ���˶���λ�ƣ�ץס��Ա���˶�ʱ��������˶���ʱ������������ֹͣ�����ж�Ա��λ�ƣ�ͨ��λ�ƹ�ϵ�ж�ǰ���Ա�Ƿ���������δ�ϣ�ǰ���Ա���������ϣ����λ�ƹ�ʽ������������˶���ʱ�䣬�Ӷ��ó�������ʱ�䣮
��� �⣨1����֪����ij��ٶ�Ϊv1=12m/s�����ٶȴ�СΪa1=2m/s2
�������ȼ����˶���ʱ��Ϊ��t1=$\frac{{v}_{1}}{{a}_{1}}$=$\frac{12}{2}s$=6s
���x1=$\frac{{v}_{1}}{2}{t}_{1}=\frac{12}{2}��6m$=36m
��2����֪ǰ���Ա�ļ��ٶ�Ϊa2=2m/s2������ٶ�Ϊv2=8m/s��ǰ���Ա���ȼ����˶��ﵽ����ٶȵ�ʱ���λ�Ʒֱ�Ϊ��
t2=$\frac{{v}_{2}}{{a}_{2}}=\frac{8}{2}s$=4s
x2=$\frac{{v}_{2}}{2}{t}_{2}=\frac{8}{2}��4m$=16m
֮��ǰ���Ա������ֱ���˶���������ֹͣ�˶�ʱ����λ��Ϊ��x3=v2��t1-t2��=16m
����x2+x3��x1��������ֹͣ�˶�ʱ��ǰ���Աû��������
Ȼ��ǰ���Ա����������ٶ������˶�������
���ù�ʽx1-��x2+x3��=v2t3��
�������ݽ�ã�t3=0.5s
ǰ���Ա�������ʱ��t=t1+t3=6.5s��
�𣺣�1������ӿ�ʼ���ȼ����˶���ͣ������λ��Ϊ36m��
��2������ֹͣ�˶�ʱ��ǰ���Աû��������ǰ���Ա�������ʱ������Ϊ6.5s��
���� ���⿼���˶�ѧ�е������⣬�ؼ�����������˶����ɣ�����˶�ѧ��ʽ�����⣬��ʱ������������ʹ������Ӽ�ݣ�

 �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д� ��������ϵ�д�
��������ϵ�д�| A�� | 2015��9��3��10��00��00��ʱ���� | |
| B�� | ��������ʽ������ʱ50������ָʱ�� | |
| C�� | �о�ͽ�������н�ʱ�����Խ��������ӿ����ʵ� | |
| D�� | �ڶ����н�ʱ������ͽ�����ӵ�ƽ���ٶȲ���ͬ |
| A�� | �� | B�� | ���� | C�� | ���� | D�� | �� |
| A�� | $\frac{2��x��{t}_{1}-{t}_{2}��}{{t}_{1}{t}_{2}��{t}_{1}+{t}_{2}��}$ | B�� | $\frac{��x��{t}_{1}-{t}_{2}��}{{t}_{1}{t}_{2}��{t}_{1}+{t}_{2}��}$ | ||
| C�� | $\frac{2��x��{t}_{1}+{t}_{2}��}{{t}_{1}{t}_{2}��{t}_{1}-{t}_{2}��}$ | D�� | $\frac{��x��{t}_{1}+{t}_{2}��}{{t}_{1}{t}_{2}��{t}_{1}-{t}_{2}��}$ |
 ��ͼ��ʾ������A��һ���ij��ٶ��شֲ�б���ϻ���б��̶�������������A���ϻ������У�����˵����ȷ���ǣ�������
��ͼ��ʾ������A��һ���ij��ٶ��شֲ�б���ϻ���б��̶�������������A���ϻ������У�����˵����ȷ���ǣ�������| A�� | ����A�ܵ�������֧����������Ħ���� | |
| B�� | ����A�ܵ�������֧��������б�����ϵ�����������Ħ���� | |
| C�� | ����A���ܵ�Ħ����������б������ | |
| D�� | ����A��б���ѹ�������������ڴ�ֱ��б�淽��ķ��� |
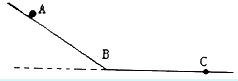 ��ͼ��ʾ�������ɾ�ֹ��A����б���ȼ����»��������ˮƽ�������ȼ����˶������ֹͣ��C�㣬��֪AB=6m��BC=9m�������˶���ʱ10s����AB�κ�BC���˶��ļ��ٶȴ�С��
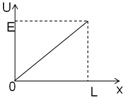
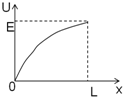
��ͼ��ʾ�������ɾ�ֹ��A����б���ȼ����»��������ˮƽ�������ȼ����˶������ֹͣ��C�㣬��֪AB=6m��BC=9m�������˶���ʱ10s����AB�κ�BC���˶��ļ��ٶȴ�С��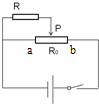 ��ͼ��ʾ�����ص���R����������������ֵR0����Դ�綯��E�����費�ƣ�xΪ��������aP�ij��ȣ�UΪ����R���˵�ѹ��LΪ�����������ܳ���������U-xͼ���ϸõ�·���ǣ�������
��ͼ��ʾ�����ص���R����������������ֵR0����Դ�綯��E�����費�ƣ�xΪ��������aP�ij��ȣ�UΪ����R���˵�ѹ��LΪ�����������ܳ���������U-xͼ���ϸõ�·���ǣ�������