Question

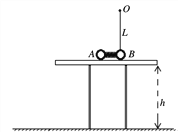
【题目】如图所示，长l＝0.2 m的细线上端固定在O点，下端连接一个质量为m＝0.5 kg的小球，悬点O距地面的高度H＝0.35 m，开始时将小球提到O点而静止，然后让它自由下落，当小球到达使细线被拉直的位置时，刚好把细线拉断，再经过t＝0.1 s落到地面，如果不考虑细线的形变，g＝10 m/s2，试求：

(1)细线拉断前、后小球的速度大小v1和v2；

(2)假设细线由拉直到断裂所经历的时间为Δt＝0.1 s，试确定细线的平均张力F的大小。

Answer 1

【答案】（1）1m/s；（2）10N

【解析】

(1) 细线拉断前，小球下落过程机械能守恒：

得

设细线断后球速为v2，方向竖直向下，由H-l＝v2t＋gt2，

可得：v2＝1 m/s

(2) 设细线的平均张力为F，方向竖直向上．取竖直向上为正方向，

由动量定理可得： (F－mg)Δt＝－mv2－(－mv1)

解得：F＝＋mg＝10N.