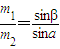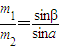题目内容
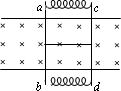
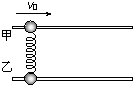如图所示，两根位于同一竖直平面内足够长的水平光滑长杆，上、下两杆上分别套着质量相等的甲、乙两金属球，两球之间用一轻质弹簧相连．开始时乙在甲的正下方，且弹簧刚好无弹力．现给甲一个水平向右的初速度v0，此后两球可在杆上无摩擦地滑动．下列叙述中正确的是（ ）| A、甲、乙两球的动量之和保持不变 | B、甲、乙两球的动能之和保持不变 | C、当甲球的速度为零时，乙球刚好位于甲球的正下方 | D、甲球的速度从v0减小至零的过程中，弹簧的弹性势能先增大后减小 |
分析：结合系统动量守恒的条件得出甲乙两球动量守恒，抓住系统机械能不变，判断甲乙两球动能之和的变化．根据动量守恒求出甲球速度为零时，乙球的速度，从而确定乙球所处的位置．根据弹簧长度的变化判断弹簧弹性势能的变化．
解答：解：A、甲乙两球组成的系统所受的外力之和为零，则甲乙两球动量守恒，则甲乙两球的动量之和保持不变．故A正确．
B、甲乙两球和弹簧组成的系统机械能守恒，弹簧的弹性势能变化，则甲乙两球的动能之和在变化．故B错误．
C、根据动量守恒定律得，甲球的速度为零时，乙球的速度为v0，速度最大，在甲球的正下方．故C正确．
D、甲球的速度从v0减小至零的过程中，弹簧先伸长再恢复到原长，则弹簧的弹性势能先增大后减小．故D正确．
故选：ACD．
B、甲乙两球和弹簧组成的系统机械能守恒，弹簧的弹性势能变化，则甲乙两球的动能之和在变化．故B错误．
C、根据动量守恒定律得，甲球的速度为零时，乙球的速度为v0，速度最大，在甲球的正下方．故C正确．
D、甲球的速度从v0减小至零的过程中，弹簧先伸长再恢复到原长，则弹簧的弹性势能先增大后减小．故D正确．
故选：ACD．
点评：解决本题的关键知道甲乙两球系统动量守恒，甲乙两球和弹簧组成的系统机械能守恒．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
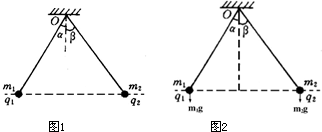
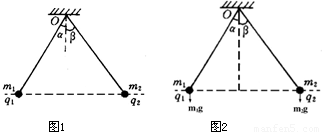
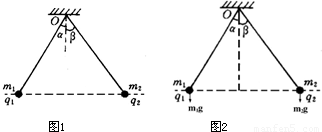
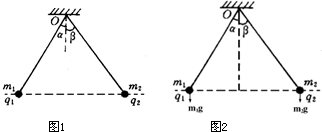辨析题：如图所示，两个质量分别为m1、m2，带电量分别为q1、q2的金属小球，用两根绝缘轻绳悬挂于同一点O．平衡时，两球恰好位于同一水平面上．轻绳与竖直方向夹角分别为α、β，请确定金属小球质量m1、m2与夹角α、β的关系式．
