题目内容
9. 在光滑的水平轨道上有两个的小球A和B(均可看作质点),质量分别为m和2m,当两球心间的距离大于L时,两球之间无相互作用力;当两球心间的距离等于或小于L时,两球间存在相互作用的恒定斥力F.设A球从远离B球处以速度v0沿两球连心线向原来静止的B球运动,如图所示.欲使两球不发生接触,v0必须满足什么条件?
在光滑的水平轨道上有两个的小球A和B(均可看作质点),质量分别为m和2m,当两球心间的距离大于L时,两球之间无相互作用力;当两球心间的距离等于或小于L时,两球间存在相互作用的恒定斥力F.设A球从远离B球处以速度v0沿两球连心线向原来静止的B球运动,如图所示.欲使两球不发生接触,v0必须满足什么条件?
分析 应用牛顿第二定律求出球的加速度,然后应用匀变速运动的运动规律求出球的位移,然后求出初速度需要满足的条件.
解答 解:两球不发生接触的条件:v1=v2,L+x2-x1>0.
由牛顿第二定律得:
A球:a1=$\frac{F}{m}$,a2=$\frac{F}{2m}$,
由速度公式得:v1=v0-a1t,v2=a2t,
由位移公式得:x1=v0t-$\frac{1}{2}$a1t2,x2=$\frac{1}{2}$a2t2,
解得:v0<$\sqrt{\frac{3FL}{m}}$;
答:v0必须满足的条件是:v0<$\sqrt{\frac{3FL}{m}}$.
点评 解决本题的关键知道两球速度相等时,有最短距离,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
17.以下说法正确的是( )
| A. | 只有受到一个方向不断改变的力,物体才可能做曲线运动 | |
| B. | 向心加速度是描述线速度大小变化快慢的物理量 | |
| C. | 物体做曲线运动时,其加速度一定改变 | |
| D. | 物体速度方向与所受合外力方向不在一条直线上,物体才可能做曲线运动 |
4.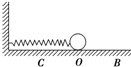 如图所示,小球在B、C之间做简谐运动,O为BC间的中点,B、C间的距离为10cm,则下列说法正确的是( )
如图所示,小球在B、C之间做简谐运动,O为BC间的中点,B、C间的距离为10cm,则下列说法正确的是( )
 如图所示,小球在B、C之间做简谐运动,O为BC间的中点,B、C间的距离为10cm,则下列说法正确的是( )
如图所示,小球在B、C之间做简谐运动,O为BC间的中点,B、C间的距离为10cm,则下列说法正确的是( )| A. | 小球的最大位移是10cm | |
| B. | 只有在B、C两点时,小球的振幅是5cm,在O点时,小球的振幅是0 | |
| C. | 无论小球在任何位置,它的振幅都是10cm | |
| D. | 从任意时刻起,一个周期内小球经过的路程都是20 cm |
14.关于功的概念,下列说法中正确的是( )
| A. | 力对物体做功越多,说明力一定越大 | |
| B. | 力对物体做功越少,说明物体的位移一定越小 | |
| C. | 力对物体不做功,说明物体一定没有移动 | |
| D. | 物体发生了位移,不一定有力对它做功 |
1.如图甲为远距离输电示意图,变压器均为理想变压器.升压变压器原副线圈匝数比为1:100,其输入电压如图乙所示,远距离输电线的总电阻为100Ω.降压变压器右侧部分为一火警报警系统原理图,其中R1为一定值电阻,R2为用半导体热敏材料制成的传感器,当温度升高时其阻值变小.电压表V显示加在报警器上的电压(报警器未画出).未出现火警时,升压变压器的输入功率为750kW.下列说法中正确的有( )
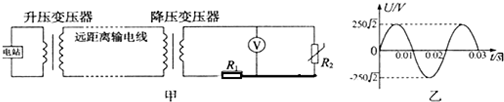

| A. | 降压变压器副线圈输出的交流电频率为100Hz | |
| B. | 远距离输电线路损耗功率为180kw | |
| C. | 当传感器R2所在处出现火警时,输电线上的电流变大 | |
| D. | 当传感器R2所在处出现火警时,电压表V的示数变大 |
19.以一定的初速度竖直向上抛出质量为m的小球,它上升的最大高度为h,空气阻力的大小恒为f.则从抛出点至回到原出发点的过程中,各力做功的情况正确的是( )
| A. | 重力做的功为零 | B. | 空气阻力做的功为-2fh | ||
| C. | 空气阻力做的功为2fh | D. | 物体克服重力做的功为-mgh |

 某游戏装置放在竖直平面内,如图所示,装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成,控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入,最后小球将由圆轨道的最高点D水平抛出,落入卡槽中得分,圆弧半径为R,O′为圆弧的圆心,C为圆弧轨道最低点,抛物线轨道上A点在坐标轴的原点O上,轨道与圆弧相切于B点,抛物线轨道方程为y=ax2(0<a<$\frac{1}{4R}$),∠BO′C=θ,x轴恰好将半径O′D分成相等的两半,交点为P,x轴与圆弧交于Q点,则:
某游戏装置放在竖直平面内,如图所示,装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成,控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入,最后小球将由圆轨道的最高点D水平抛出,落入卡槽中得分,圆弧半径为R,O′为圆弧的圆心,C为圆弧轨道最低点,抛物线轨道上A点在坐标轴的原点O上,轨道与圆弧相切于B点,抛物线轨道方程为y=ax2(0<a<$\frac{1}{4R}$),∠BO′C=θ,x轴恰好将半径O′D分成相等的两半,交点为P,x轴与圆弧交于Q点,则: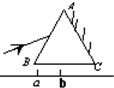 如图所示,三棱镜的AC面镀有反射膜,一束白光射向AB面,经棱镜折射后,在屏幕的ab段形成彩色光带,则a点的颜色是红,b点的颜色是紫.
如图所示,三棱镜的AC面镀有反射膜,一束白光射向AB面,经棱镜折射后,在屏幕的ab段形成彩色光带,则a点的颜色是红,b点的颜色是紫.