题目内容
3.有一条南北流向的大河,两岸平直,河水均匀流动、流速恒为v,若驾着小船渡河,先从东岸到西岸,行驶路线始终与河岸垂直,后从西岸回到东岸,船头指向始终与河岸垂直.先、后两次所用时间的比值为n,船在静水中的速度大小为( )| A. | $\frac{nv}{\sqrt{1-{n}^{2}}}$ | B. | $\frac{v}{\sqrt{1-{n}^{2}}}$ | C. | $\frac{v}{\sqrt{{n}^{2}-1}}$ | D. | $\frac{nv}{\sqrt{{n}^{2}-1}}$ |
分析 根据船头指向始终与河岸垂直,结合运动学公式,可列出河宽与船速的关系式,当路线与河岸垂直时,可求出船过河的合速度,从而列出河宽与船速度的关系,进而即可求解.
解答 解:设船渡河时的速度为vc;当从东岸到西岸时,行驶路线与河岸垂直,则有:t1=$\frac{d}{{v}_{合}}$;
此时的船的合速度为:v合=$\sqrt{{v}_{c}^{2}-{v}^{2}}$;
当从西岸回到东岸时,船头指向始终与河岸垂直,则有:t2=$\frac{d}{{v}_{c}}$;
由于先、后两次所用时间的比值为n,
所以小船在静水中的速度大小为:vc=nv合=n$\sqrt{{v}_{c}^{2}-{v}^{2}}$;
解得:vc=$\frac{nv}{\sqrt{{n}^{2}-1}}$,故D正确,ABC错误;
故选:D.
点评 解决本题的关键知道分运动与合运动具有等时性,以及知道各分运动具有独立性,互不干扰.

练习册系列答案
相关题目
5.我国“北斗”卫星导航技术堪比美国GPS.已知“北斗”卫星导航系统中某卫星的运行周期约为12小时,则此卫星与北斗导航系统中的地球同步卫星相比较( )
| A. | 线速度更大 | B. | 角速度更大 | C. | 轨道半径更大 | D. | 向心加速度更大 |
18.下说法正确的是( )
| A. | 同一物体在地球(视为均匀球体)上的任何位置所受重力都相等 | |
| B. | 同一物体在地球(视为均匀球体)上的任何位置所受万有引力的大小都相等 | |
| C. | 开普勒指出所有行星都在同一平面内以太阳为公共焦点的椭圆轨道上运动 | |
| D. | 牛顿发现万有引力定律并通过扭秤实验测出引力常量 |
15.一条船航行时船头正对河岸,它在静水中航行速度大小一定,当船行驶到河中心时,河水流速突然增大,这使得该船( )
| A. | 渡河时间不变 | B. | 渡河时间变大 | C. | 速度不变 | D. | 速度变小 |
 2012年,我国宣布北斗星导航系统正式进入商业运行.北斗卫星导航系统空间段由5颗静止轨道卫星和27颗中地球轨道卫星、3颗倾斜同步轨道卫星组成.该系统具有导航、定位等功能.如图为“北斗”系统中某一工作卫星,它绕地心做匀速圆周运动,轨道半径为r,某时刻位于轨道上的A位置,若卫星顺时针运行,经过一段时间运动到B位置,且与地球连线的夹角为60°,地球表面处的重力加速度为g,地球半径为R,万有引力常量为G.求:
2012年,我国宣布北斗星导航系统正式进入商业运行.北斗卫星导航系统空间段由5颗静止轨道卫星和27颗中地球轨道卫星、3颗倾斜同步轨道卫星组成.该系统具有导航、定位等功能.如图为“北斗”系统中某一工作卫星,它绕地心做匀速圆周运动,轨道半径为r,某时刻位于轨道上的A位置,若卫星顺时针运行,经过一段时间运动到B位置,且与地球连线的夹角为60°,地球表面处的重力加速度为g,地球半径为R,万有引力常量为G.求: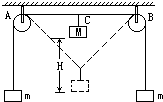 如图所示,将细绳绕过两个定滑轮A和B,绳的两端各挂一个质量为m的砝码,AB的中点C处挂一个质量为M的物体,且M<2m,AB间的距离为2l,把M从静止放开,求:
如图所示,将细绳绕过两个定滑轮A和B,绳的两端各挂一个质量为m的砝码,AB的中点C处挂一个质量为M的物体,且M<2m,AB间的距离为2l,把M从静止放开,求: