题目内容
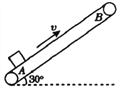
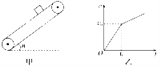
【题目】如图甲所示，足够长的传送带与水平面夹角为θ，正以某一速度匀速转动，在传送带上某位置轻轻放置一小木块，小木块与传送带间动摩擦因数为μ，小木块速度随时间变化关系如图乙所示，v0、t0已知，则
A. 传送带一定顺时针转动
B. 传送带的速度等于v0
C. μ＝
-tan θ
D. t0后木块的加速度为
-2gsin θ
【答案】BC
【解析】若传送带顺时针转动，当滑块下滑（
），将一直匀加速到底端而且加速度不变；若滑块上滑（
），先匀加速运动，在速度相等后将匀速运动，两种均不符合运动图象，故传送带是逆时针转动，故A错误；只有当滑块的速度等于传送带的速度时，滑块所受的摩擦力变成斜向上，故传送带的速度等于v0，故B正确；滑块在0～t0内，滑动摩擦力向下做匀加速下滑，由牛顿第二定律： 
，解得： 
，由图可知， 
，联立解得： 
，故C正确；达到共速后，由牛顿第二定律： 
，解得： 
，代入μ值得： 
，故D错误。所以BC正确，AD错误。
练习册系列答案
阅读快车系列答案
相关题目
