题目内容
1.天文学家新发现了太阳系外的一颗行星.这颗行星的体积是地球的1.8倍,质量是地球的25倍.已知近地卫星绕地球运动的周期约为1.4小时,引力常量G=6.67×10- 11N•m2/kg2,由此估算该行星的平均密度约为( )| A. | 1.8×103kg/m3 | B. | 5.6×103kg/m3 | C. | 7.7×104kg/m3 | D. | 2.9×104kg/m3 |
分析 根据万有引力提供圆周运动的向心力知,只要知道近地卫星绕地球做圆周运动的周期就可以估算出地球的密度,再根据行星与地球的质量关系和半径关系直接可得行星密度与地球密度之间的关系,从而求解即可.
解答 解:首先根据近地卫星绕地球运动的向心力由万有引力提供有:$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}R}{{T}^{2}}$,
可求出地球的质量为:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$.
又据M=$\frac{4}{3}π{R}^{3}ρ$得地球的密度为:${ρ}_{地}=\frac{3π}{G{T}^{2}}$=5.5×103kg/m3
又因为该行星质量是地球的25倍,体积是地球的4.7倍,则其密度为地球的:
${ρ}_{行}=\frac{25M}{1.8V}=13.89×$5.5×103≈7.7×104kg/m3.
故选:C
点评 根据近地卫星的向心力由万有引力提供,再根据质量和体积及密度的关系可知,地球的平均密度${ρ}_{地}=\frac{3π}{G{T}^{2}}$,从而可以算出地球的质量,再根根据行星质量与体积与地球的关系可以估算出行星的密度.熟练掌握万有引力提供向心力的表达式,是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )
质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )
 质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )
质量为m可视为质点的物体,在所受合外力F作用下运动的速度v随时间变化的规律如图所示,合外力的方向始终在一条直线上.已知t=0时质点的速度为零,在图示的t1、t2、t3和t4各时刻中,下列说法正确的是( )| A. | t1后物体运动的速度方向改变 | |
| B. | t1到t3时间内物体受到的合外力与选定的正方向相反 | |
| C. | t2时刻物体的速度为零、合外力也为零 | |
| D. | t2时刻物体又回到出发点 |
10.下列关于电场线的论述,正确的是( )
| A. | 电场线的切线方向就是正检验电荷在该点的受力方向 | |
| B. | 电场线的疏密程度可以表示电场强度E的大小 | |
| C. | 电场线是直线的地方就是匀强电场 | |
| D. | 画有电场线的地方有电场,没有画电场线的地方没有电场 |
11.下列说法中正确的是( )
| A. | 变化的电场周围空间产生的磁场一定是变化的 | |
| B. | 变化的磁场周围空间产生的电场一定是变化的 | |
| C. | 均匀变化的磁场周围空间产生恒定的电场 | |
| D. | 振荡电场周围空间产生的磁场也是振荡的 |
 如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m.现有一个质量m=5kg的旅行包(视为质点)以v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=0.6.皮带轮与皮带之间始终不打滑.g取10m/s2.
如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m.现有一个质量m=5kg的旅行包(视为质点)以v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=0.6.皮带轮与皮带之间始终不打滑.g取10m/s2.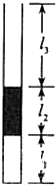 如图,一上端开口、下端封闭的细长玻璃管竖直放置.玻璃管的下部封有长l1=25.0cm的空气柱,中间有一段长为l2=25.0cm的水银柱,上部空气柱的长度l3=40.0cm.已知大气压强为P0=75.0cmHg.现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为$l_1^'$=20.0cm.假设活塞下推过程中没有漏气,试求:
如图,一上端开口、下端封闭的细长玻璃管竖直放置.玻璃管的下部封有长l1=25.0cm的空气柱,中间有一段长为l2=25.0cm的水银柱,上部空气柱的长度l3=40.0cm.已知大气压强为P0=75.0cmHg.现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为$l_1^'$=20.0cm.假设活塞下推过程中没有漏气,试求: 如图所示,水平放置的两平行金属导轨间距L=0.5m,所接电源的电动势E=1.5V,内阻r=0.2Ω,金属棒的电阻R=2.8Ω,与平行导轨垂直,其余电阻不计,金属棒处于磁感应强度B=2.0T、方向与水平方向成60°角的匀强磁场中.在接通电路后金属棒还是静止,则
如图所示,水平放置的两平行金属导轨间距L=0.5m,所接电源的电动势E=1.5V,内阻r=0.2Ω,金属棒的电阻R=2.8Ω,与平行导轨垂直,其余电阻不计,金属棒处于磁感应强度B=2.0T、方向与水平方向成60°角的匀强磁场中.在接通电路后金属棒还是静止,则