题目内容
4. 如图所示的竖直直角坐标平面xoy内有两条过原点的射线OA和OB与x轴的正半轴和负半轴都成45°角,在x轴上方∠AOB区域间分布着方向垂直纸面向外大小为B1的匀强磁场,在x轴的下方存在着方向垂直纸面向外大小为B2=$\frac{mv}{qL}$的匀强磁场,现有一质量为m,带电量为+q的带电粒子以速度v从位于直线OA上的P(L,L)点竖直向下射出,经过测量发现,此粒子每经过相同的时间T会回到P点,(不计粒子重力)
如图所示的竖直直角坐标平面xoy内有两条过原点的射线OA和OB与x轴的正半轴和负半轴都成45°角,在x轴上方∠AOB区域间分布着方向垂直纸面向外大小为B1的匀强磁场,在x轴的下方存在着方向垂直纸面向外大小为B2=$\frac{mv}{qL}$的匀强磁场,现有一质量为m,带电量为+q的带电粒子以速度v从位于直线OA上的P(L,L)点竖直向下射出,经过测量发现,此粒子每经过相同的时间T会回到P点,(不计粒子重力)(1)求匀强磁场$\frac{B_1}{B_2}$之比;
(2)求粒子相邻两次经过P点的时间间隔T;
(3)若保持B2不变,而∠AOB间的磁场方向不变,现从P点向下发射两个速度在0-$\frac{v}{2}$范围内与原来相同的带电粒子(不计两个粒子间的相互作用力),它们进入∠AOB间的匀强磁场后都要经过P点,求∠AOB间的磁感应强度的B'1的大小.
(4)请判断:题(3)中若从P点向下发射的是一群速度在0-$\frac{v}{2}$范围内与原来比荷相同的带电粒子(不计粒子间的相互作用力)它们进入B1′的匀强磁场后能否都经过P点.(不需要写理由)
分析 (1)粒子从P点向下,运动过程的轨迹图画出来,根据对称性,在上下两磁场中匀速圆周运动的半径相等
(2)求出粒子在上下磁场中的轨道半径,圆周运动的规律求在磁场中的时间,在磁场外用匀速运动规律求时间
(3)画出粒子运动的轨迹,通过几何关系可知在上面磁场中圆周运动半径是下方磁场中圆周运动半径的2倍,粒子在下方磁场中运动半个周期,在上方磁场中运动四分之一圆周,再由半径公式得出磁感应强度之间的关系,从而求出上方磁场的磁感应强度
(4)同(3)分析得出在$0-\frac{v}{2}$范围的所有粒子运动只是轨道不同,运动的规律一样,从P先向下匀速,再圆周运动半周,然后匀速,进入第一象限磁场做四分之一圆周,所以都能到P点
解答 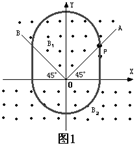 解:(1)由P点射出的粒子先做匀速直线运动进入匀强磁场${B}_{2}^{\;}$中,设匀速圆周运动的半径为${R}_{2}^{\;}$,
解:(1)由P点射出的粒子先做匀速直线运动进入匀强磁场${B}_{2}^{\;}$中,设匀速圆周运动的半径为${R}_{2}^{\;}$,
由$qv{B}_{2}^{\;}=m\frac{{v}_{\;}^{2}}{{R}_{2}^{\;}}$得:${R}_{2}^{\;}=\frac{mv}{q{B}_{2}^{\;}}$=L
粒子每经过相同时间T会回到P点必满足在匀强磁场${B}_{1}^{\;}$中半径${R}_{1}^{\;}$大小为:
$qv{B}_{1}^{\;}=m\frac{{v}_{\;}^{2}}{{R}_{1}^{\;}}$
得:${R}_{1}^{\;}=\frac{mv}{q{B}_{1}^{\;}}=L$
$\frac{{B}_{1}^{\;}}{{B}_{2}^{\;}}=1$
(2)带电粒子在无匀强磁场运动的时间为:${t}_{1}^{\;}=\frac{2L}{v}$
在匀强磁场${B}_{2}^{\;}$中运动时间为:${t}_{2}^{\;}=\frac{πL}{v}$
在匀强磁场${B}_{1}^{\;}$中运动时间为:${t}_{3}^{\;}=\frac{πL}{v}$
故粒子相邻两次经过P点的时间间隔为:$T={t}_{1}^{\;}+{t}_{2}^{\;}+{t}_{3}^{\;}=\frac{2L}{v}+\frac{2πL}{v}$
(3)从P点向下发射速度为${v}_{x}^{\;}$满足范围为$0-\frac{v}{2}$与原来相同的带电粒子,由于保持${B}_{2}^{\;}$不变,当速度v时半径为L,则速度为$0-\frac{v}{2}$的粒子必定经过半个周期后在x轴正半轴间返回∠A OB间磁场,如图2所示,进入${B}_{1}^{'}$匀强磁场后都要经过P点,则在${B}_{1}^{'}$磁场中运动的半径为${B}_{2}^{\;}$磁场中运动半径的两倍,即$2\frac{m{v}_{x}^{\;}}{q{B}_{2}^{\;}}=\frac{m{v}_{x}^{\;}}{q{B}_{1}^{'}}$
OB间磁场,如图2所示,进入${B}_{1}^{'}$匀强磁场后都要经过P点,则在${B}_{1}^{'}$磁场中运动的半径为${B}_{2}^{\;}$磁场中运动半径的两倍,即$2\frac{m{v}_{x}^{\;}}{q{B}_{2}^{\;}}=\frac{m{v}_{x}^{\;}}{q{B}_{1}^{'}}$
得:$\frac{{B}_{1}^{'}}{{B}_{2}^{\;}}=\frac{1}{2}$
即:${B}_{1}^{'}=\frac{{B}_{2}^{\;}}{2}=\frac{mv}{2qL}$
(4)能
答:(1)匀强磁场$\frac{{B}_{1}}{{B}_{2}}$之比为$\frac{{B}_{1}^{\;}}{{B}_{2}^{\;}}=1$
(2)粒子相邻两次经过P点的时间间隔$T=\frac{2L}{v}+\frac{2πL}{v}$
(3)∠AOB间的磁感应强度的B′1的大小为${B}_{1}^{'}=\frac{mv}{2qL}$
(4)能
点评 根据粒子在洛伦兹力作用下做圆周运动,依据几何特性作图时解题关键,本题第三问、第四问重点考查作图能力,画轨迹是解决这类问题的关键.


| A. | 乙图中c点位置代表滑块速度最大,且弹簧的压缩量为4cm | |
| B. | 从刚释放至分离时,滑块上滑距离x=7cm | |
| C. | 滑块与斜面间的动摩擦因数μ=0.25 | |
| D. | 乙图中d点位置代表滑块与弹簧刚好分离,在滑块与弹簧分离之前,滑块一直在做加速运动 |
| A. | a 与 vt方向一定相反 | B. | a 与△v方向一定相反 | ||
| C. | a 与 v0方向一定相同 | D. | a 与△v方向一定相同 |
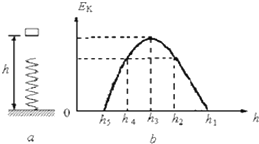 如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法不正确的是( )
如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法不正确的是( )| A. | 小物体下降至高度h3时,弹簧形变量为0 | |
| B. | 小物体下落至高度h5时,加速度为0 | |
| C. | 小物体从高度h2下降到h4,弹簧的弹性势能增加了$\frac{{m}^{2}{g}^{2}}{k}$ | |
| D. | 小物体从高度h1下降到h5,弹簧的最大弹性势能为mg(h1-h5) |
 如图所示表示撑杆跳高运动的几个阶段:助跑、撑杆起跳、越横杆、落地(未画出).在这几个阶段中有关能量转化情况的说法,正确的是( )
如图所示表示撑杆跳高运动的几个阶段:助跑、撑杆起跳、越横杆、落地(未画出).在这几个阶段中有关能量转化情况的说法,正确的是( )| A. | 助跑阶段,身体中的化学能转化为人和杆的动能 | |
| B. | 起跳时,人的动能和化学能转化为人和杆的势能 | |
| C. | 越过横杆后,人的重力势能转化为动能 | |
| D. | 落地后,人的能量消失了 |
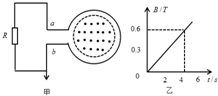 如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,b端接地,则下列说法正确的是( )| A. | 圆形线圈中产生的感应电动势E=6V | |
| B. | 电阻R两端的电压为4.5V | |
| C. | 通过电阻R的电流为I=1.5A | |
| D. | 在0-4s时间内,b端的电势比a端的电势低 |
| A. | 重力势能恒大于零 | |
| B. | 重力做功的多少与参考平面的选取有关 | |
| C. | 放在地面上的物体,它的重力势能一定等于零 | |
| D. | 相对不同的参考平面,物体具有不同数值的重力势能,但并不影响研究有关重力势能 |
