题目内容
【题目】如图，将半径为 R 的透明半球体放在水平桌面上方，O 为球心，直径恰好水平，轴线 OO' 垂直于水平桌面。 位于 O 点正上方某一高度处的点光源 S 发出一束与 OO' 夹角 θ=60°的单色光射向半球体上的 A 点，已知透明半球体对单色光的折射率为
，光在真空中传播速度为 c，不考虑半球体内光的反射，求：
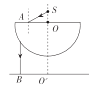
（1）求光线通过半球体后射到桌面上的位置 B（图中未画出）到 O' 的位置；
（2）求该光在半球体内传播的时间t。
【答案】ⅰ．
ⅱ． 
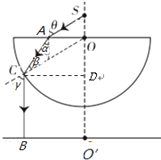
【解析】试题分析：ⅰ．光从光源S射出经半球体到达水平桌面的光路如图，光由空气射向半球体，入射角
，
折射率： 
由折射定律，有
代入数据解得： 
光由半球射入空气，由几何关系可知α+β=60°，故有：α=β=30°
又由折射定律，有
解得折射角为： 
由几何关系可知，出射光线平行于轴线OO′，垂直射到水平桌面上的B点
ⅱ．光在半球体中传播的速度为： 
由几何知识得 2ACcos30°=R
得： 
所以光在半球体中传播的时间为： 
练习册系列答案
相关题目
