题目内容
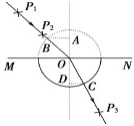
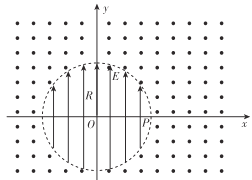
【题目】如图所示,在直角坐标系xOy内有一半径为R的圆,圆的圆心在坐标原点O处,圆内有沿y轴正方向的匀强电场,电场强度大小为E,圆外有垂直于坐标平面向外的匀强磁场。现从坐标原点O处由静止释放一个质量为m、电荷量为q的带正电的粒子,粒子经电场加速后进入磁场,并从圆与x轴的交点P处垂直电场线再次进入电场,不计粒子的重力。求:
(1)匀强磁场的磁感应强度大小;
(2)粒子从O点由静止释放到再次到达y轴运动的时间;
(3)若让粒子从坐标为(![]() ,0)的位置由静止释放,则粒子经电场加速再经磁场偏转第一次经过x轴的位置离坐标原点的距离。
,0)的位置由静止释放,则粒子经电场加速再经磁场偏转第一次经过x轴的位置离坐标原点的距离。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设粒子进入磁场时的速度大小为![]() ,粒子在电场中加速过程,根据动能定理有
,粒子在电场中加速过程,根据动能定理有
![]()
解得
![]()
粒子进入磁场后做匀速圆周运动,由题意结合几何关系可知,粒子在磁场中做匀速圆周运动的半径![]() ,设磁场的磁感应强度大小为B,根据牛顿第二定律有
,设磁场的磁感应强度大小为B,根据牛顿第二定律有
![]()
解得
![]()
(2)设粒子第一次在电场中运动的时间为![]() ,则有
,则有
![]()
解得
![]()
粒子在磁场中运动的时间
![]()
粒子从P点进入电场后做类平抛运动,设粒子到达![]() 轴时还在电场中,则有
轴时还在电场中,则有
![]() ,
,![]() ,
,![]()
解得
![]()
假设成立,因此
![]()
粒子从O点由静止释放到再次到达![]() 轴运动的时间为
轴运动的时间为
![]()
(3)粒子从坐标为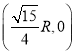 的位置由静止释放,在电场中加速的距离为
的位置由静止释放,在电场中加速的距离为
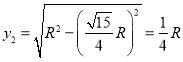
设粒子进入磁场时的速度为![]() ,根据动能定理有
,根据动能定理有
![]()
解得
![]()
设粒子在磁场中做圆周运动的半径为![]() ,由牛顿第二定律得
,由牛顿第二定律得
![]()
解得
![]()
粒子在磁场中运动的轨迹如图所示
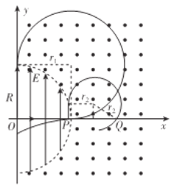
由几何关系可知,粒子在磁场中偏转第一次经过![]() 轴的位置
轴的位置![]() 点离坐标原点的距离
点离坐标原点的距离
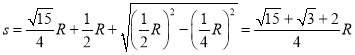

【题目】读下表:
0 | T/4 | T/2 | 3T/4 | T | |
甲 | 零 | 正向最大 | 零 | 负向最大 | 零 |
乙 | 零 | 负向最大 | 零 | 正向最大 | 零 |
丙 | 正向最大 | 零 | 负向最大 | 零 | 正向最大 |
丁 | 负向最大 | 零 | 正向最大 | 零 | 负向最大 |
如果表中给出的是做简谐运动的物体的位移x或速度与时刻的对应关系,T是振动周期,则下列选项中正确的是( )
A.若甲表示位移x,则丙表示相应的速度v
B.若乙表示位移x,则甲表示相应的速度v
C.若丙表示位移x,则甲表示相应的速度v
D.若丁表示位移x,则乙表示相应的速度v