��Ŀ����
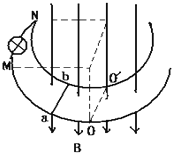
����Ŀ����ͼ��ʾ���뾶ΪR�Ĺ⻬Բ�����ABC�̶�����ֱƽ���ڣ�O��Բ�ģ�OC��ֱ��OAˮƽ��B����͵㣬A�����һ�㹻����ƽ̨MN��D��λ��A�����Ϸ�������D�����ٶ��ͷ�һ����С���Ժ��Ե�С��С���A�����Բ���������C��ɳ�����ƽ���˶�������ƽ̨MN�ϣ�P����С������MN֮ǰ�켣�Ͻ���MN��һ�㣬���ƿ�������������˵����ȷ����( )

A. ֻҪDA�ĸ߶ȴ���![]() ��С��Ϳ�������ƽ̨MN������һ��
��С��Ϳ�������ƽ̨MN������һ��
B. ��DA�߶�Ϊ2R����С��B��ʱ�Թ����ѹ��Ϊ7mg
C. С���D�˶���B�Ĺ����У������Ĺ���һֱ����
D. ��С��P��ʱ���ٶȷ�����MN�н���Ϊ30�������Ӧ��DA�߶�Ϊ4R
���𰸡�BD
��������
A����![]() ��С�����ͨ��C�����С�ٶ�
��С�����ͨ��C�����С�ٶ� ![]() ����
����![]() ��
��![]() ������С�����ͨ��C������Ӧ��DA��С�߶�����
������С�����ͨ��C������Ӧ��DA��С�߶�����![]() ��
��![]() ����
����![]() ������ƽ����Сˮƽλ��������������ƽ̨MN������һ������A������
������ƽ����Сˮƽλ��������������ƽ̨MN������һ������A������
B����DA =2R����![]() ��
��![]() ����F = 7mg����B��ȷ��
����F = 7mg����B��ȷ��
C����D��A�����ٶȷ������������һ�£������Ĺ���������A��B���ٶȷ�������������н�Խ��Խ��B��ʱ�����Ĺ���Ϊ�㣻C������
D����ͼ���� = 30������![]() ��
��![]() ��
��![]() �������h = 4R��D��ȷ��
�������h = 4R��D��ȷ��
��ѡBD��

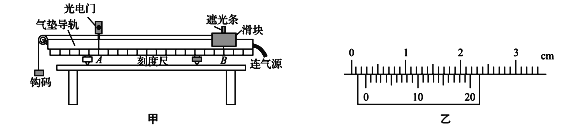
����Ŀ��ijͬѧ�����ô���ʱ�����ٶ�����ʵ���У��ô���ʱ����¼�˱�С���϶���ֽ�����˶��������ֽ����ȷ����A��B��C��D��E��F��G��7�������㣮�����ڵ��ľ�����ͼ��ʾ��ÿ�������ڵIJ�����֮���ʱ����Ϊ0.10s��

��1���Ը���ֽ���ϸ����������ľ��룬ÿ��0.10s��һ���ٶȣ����������B��C��D��E��F�����ʱС����˲ʱ�ٶȣ����������ٶ�ֵ�����±������Ҫ����3λ��Ч���֣�
vB | vC | vD | vE | vF | |
��ֵ��m/s�� | ____ | ____ | ____ | ____ | ____ |
��2����B��C��D��E��F����ʱ�̵�˲ʱ�ٶȱ���ֱ������ϵ�У�����ͼ�л���С����˲ʱ�ٶ���ʱ��仯�Ĺ�ϵͼ�ߣ�
��______________��
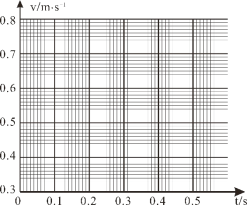
��3����v��tͼ���֪����A��ʱС����˲ʱ�ٶ�vA=________������G��ʱС����˲ʱ�ٶ�vB=________��