题目内容
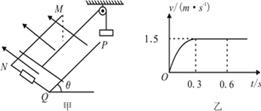
如图甲所示,一个n=10匝,面积为S=0.3m2的圆形金属线圈,其总电阻为R1="2Ω," 与R2=4Ω的电阻连接成闭合电路。线圈内存在方向垂直于纸面向里,磁感应强度按B1="2t" + 3 (T)规律变化的磁场。电阻R2两端通过金属导线分别与电容器C的两极相连.电容器C紧靠着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒。圆筒内壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径为r=0.4m.
(1)金属线圈的感应电动势E和电容器C两板间的电压U;
(2)在电容器C内紧靠极板且正对a孔的D处有一个带正电的粒子从静止开始经电容器C加速后从a孔垂直磁场B2并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒.已知粒子的比荷q/m=5×107(C/kg),该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子重力和空气阻力,则磁感应强度B2多大(结果允许含有三角函数式)。
(1) 6V ;4V (2) 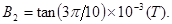 或
或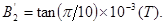
解析试题分析:(1)线圈中产生的感应电动势E= 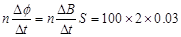 V =6V
V =6V
电容器C两板间电压U=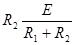 =4V
=4V
(2)据动能定理有, 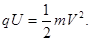
带电粒子在磁场中作匀速圆周运动,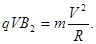
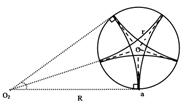
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为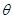 ,则由几何关系可得:
,则由几何关系可得: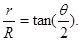
有两种情形符合题意(如图所示):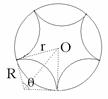
(ⅰ)情形1:每段轨迹圆弧对应的圆心角为 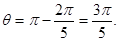
得: 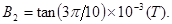
(ⅱ)情形2:每段轨迹圆弧对应的圆心角为 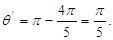
将数据代式得: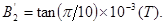
考点:此题考查法拉第电磁感应定律、欧姆定律及动能定理;考查的物理模型是匀速圆周运动。

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案下列说法中错误的是:
| A.重力对物体所做的功只跟起点和终点位置有关,跟物体的运动路径无关 |
| B.摩擦力对物体做功,也与路径无关 |
| C.物体克服重力做了多少功,重力势能就增加了多少 |
| D.物体沿不同路径从一个位置移到另一个位置克服摩擦力做功一般不相等 |
如图,细线的一端固定于O点,另一端系一小球,在水平拉力作用下,小球以恒定速率在竖直平面内由A点运动到B点,在此过程中拉力的瞬时功率变化情况是 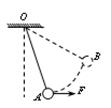
| A.逐渐增大 | B.逐渐减小 | C.先增大,后减小 | D.先减小,后增大 |
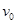 正对P点进入该电场后,从M点飞离CD边界时速度为
正对P点进入该电场后,从M点飞离CD边界时速度为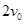 ,再经磁场偏转后又从N点垂直于CD边界回到电场区域,并恰能返回O点。已知OP间距离为
,再经磁场偏转后又从N点垂直于CD边界回到电场区域,并恰能返回O点。已知OP间距离为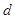 ,粒子质量为
,粒子质量为 ,电量为
,电量为 ,粒子自身重力忽略不计。试求:
,粒子自身重力忽略不计。试求:
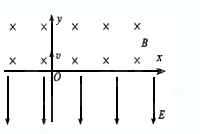
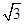 m≤x≤0的区域内有磁感应强
m≤x≤0的区域内有磁感应强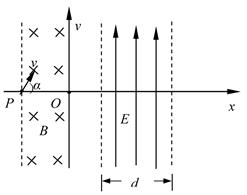
 时间打到极板上。
时间打到极板上。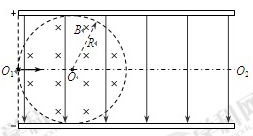
 ,g="10" m/s2,求:
,g="10" m/s2,求: